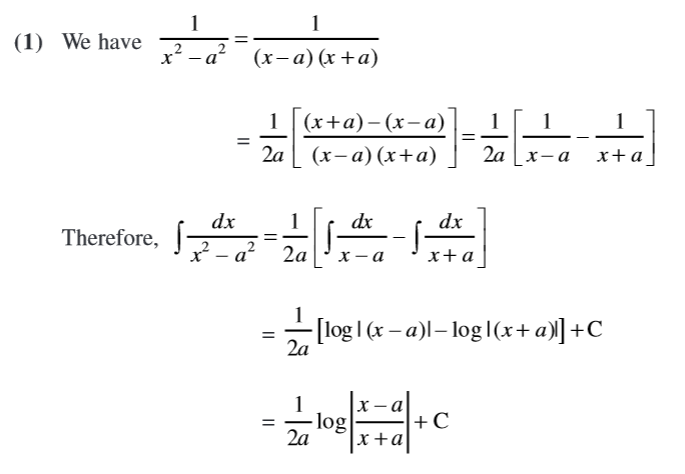The required integral is
#I = intsinx/cos(2x)dx#
The first part of the solution requires the use of the trigonometric identity #cos(2x) = 2cos^2x - 1#
This leaves you with,
#I = intsinx/(2cos^2x - 1)dx#
Let #cosx = t#
Differentiating both sides with respect to t,
#-sinx dx/dt = 1#
#=> sinxdx=-dt#
Thus,
#I = -int1/(2t^2-1)dt#
#=> I = -1/2int1/(t^2-1/2)dt#
This sort of integral has a standard result, which is
#int1/(x^2-a^2)dx = 1/(2a)ln|(x-a)/(x+a)| + C#
which I will derive once we have the answer to your question, which is
#I = -1/2[1/(2(1/sqrt(2)))ln|(t-1/sqrt2)/(t+1/sqrt2)|] + C#
#=> I = -sqrt2/4ln|(t-1/sqrt2)/(t+1/sqrt2)| + C#
Finally, replacing #t=cosx#, we get,
#intsinx/cos(2x)dx = -sqrt2/4ln|(cosx-1/sqrt2)/(cosx+1/sqrt2)|#+C
Now, for the derivation of #int1/(x^2-a^2)dx = 1/(2a)ln|(x-a)/(x+a)| + C# here's a screenshot from a textbook.