How do you find the integral of #7x^2ln(x) dx#?
2 Answers
Mar 8, 2015
I would use Integretion by Parts:
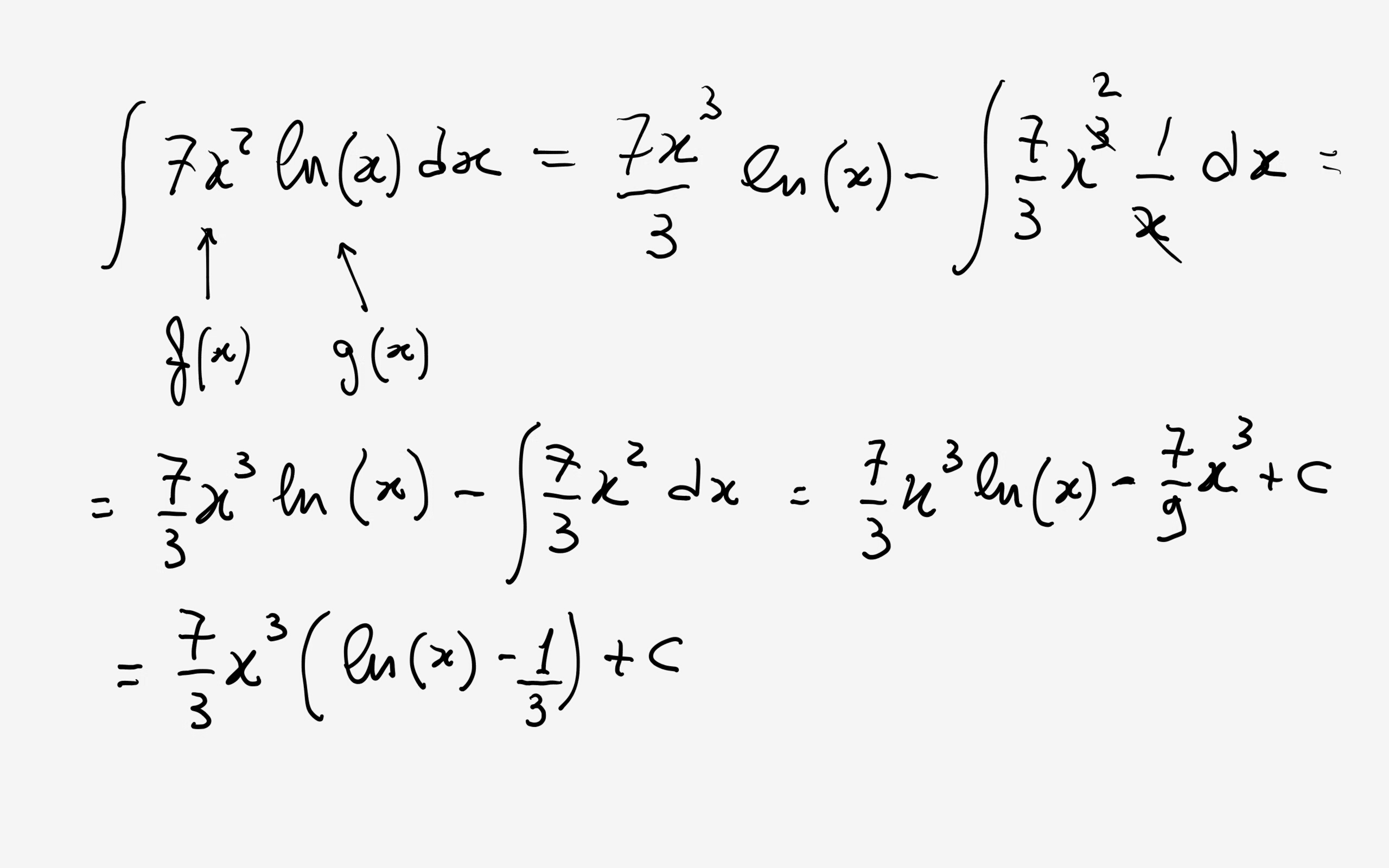
Mar 8, 2015
How: Use integration by parts.
(Any integral of the form
Details:
Let
This makes
General
Notice that the solution can be made quite general.
For example: with 5 instead of 3 the problem becomes
Note: For even better understanding, check the answers by differentiating.


