How do you find the integral of 3x (sqrt(81-x^2))?
3 Answers
Have a look:
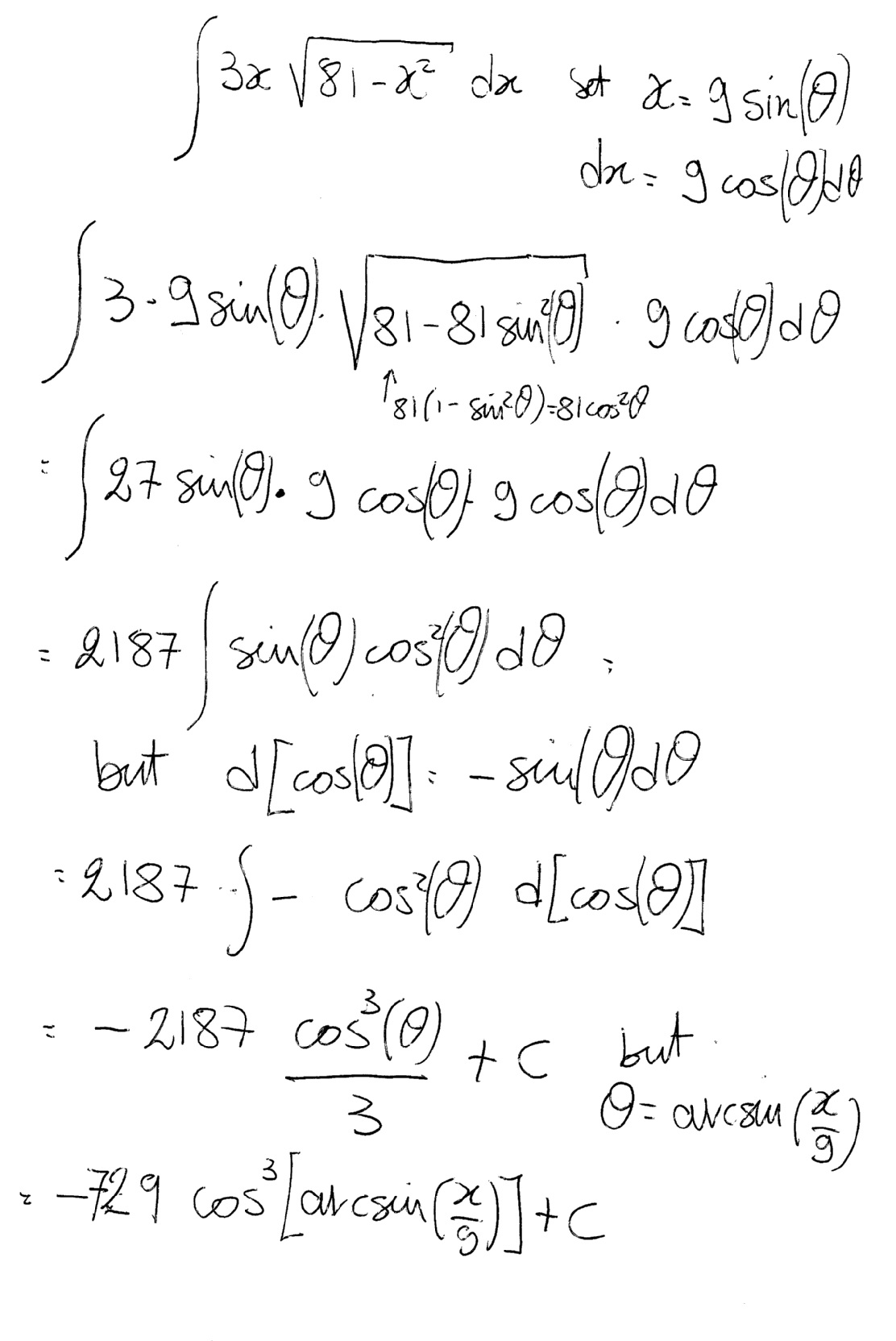
The answer using this method will look like the other, if you use:
Apr 20, 2015
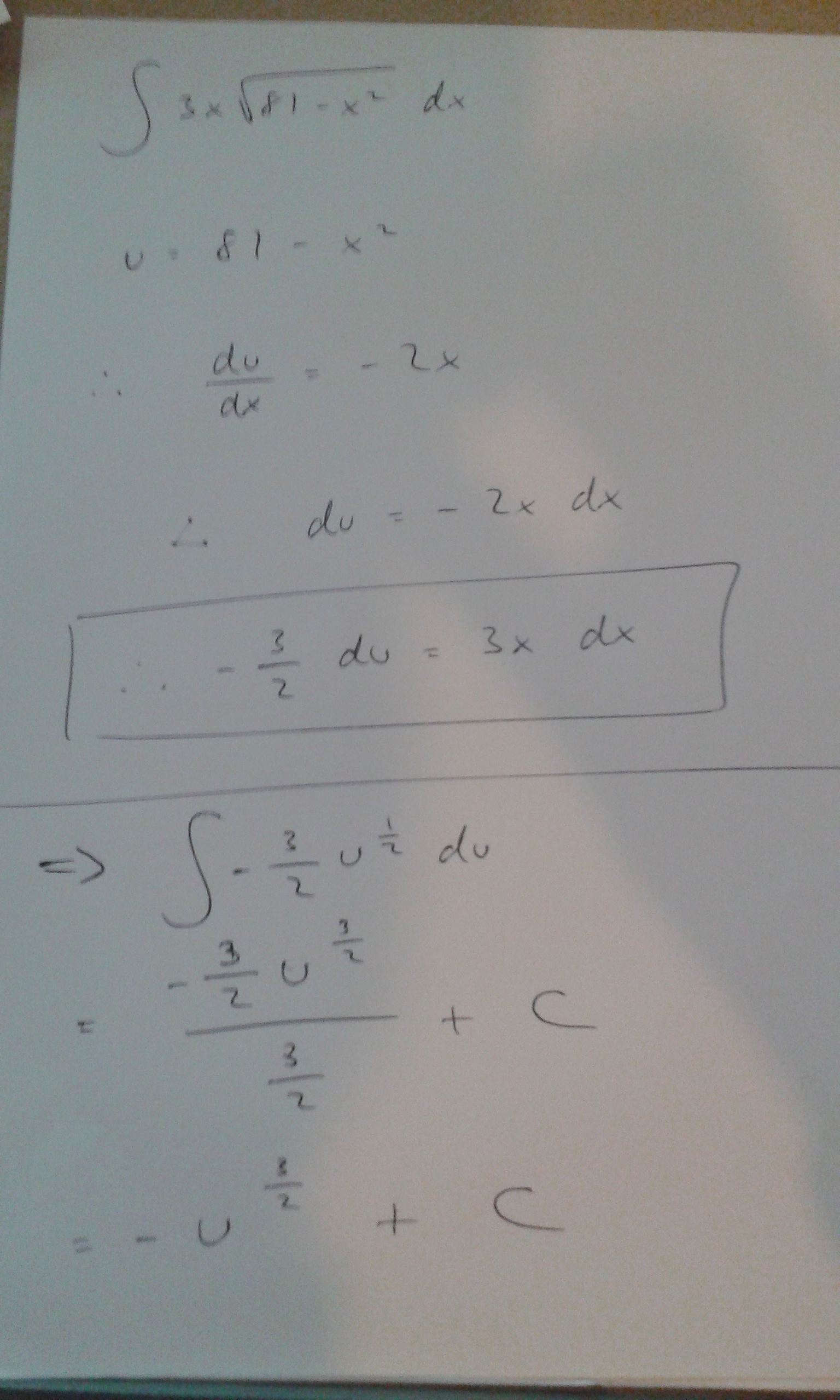
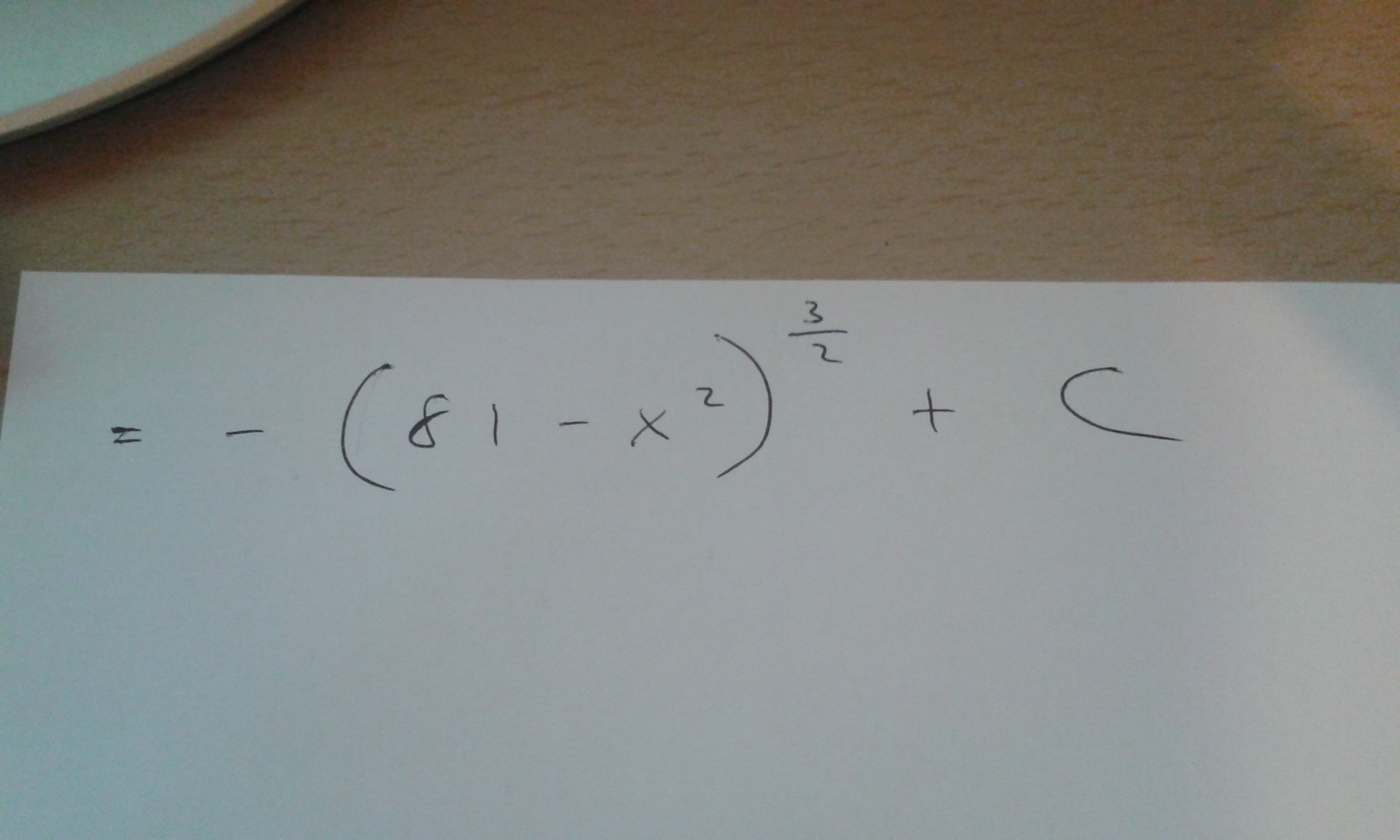
Apr 20, 2015
The answer is:
Remembering that:
than:
or, if you want




