Question

What is the difference between the cross-product and the dot-product of two vectors? or If a force of 10 Newtons at an angle of `30^circ` above horizontal is used to drag a block 6 meters, how much work is done?

Answer 1

The Cross Product is a vector
If A and B are vectors
then `A xx B` is a vector perpendicular to both A and B (that is perpendicular to the plane containing A and B if A and B are two dimensional vectors in 3D space) with magnitude equal to the area of the parallelogram with sides A and B

`AxxB = |\|A|\|* |\|B|\| *sin(theta)*n`
where `|\|V|\|` is the magnitude of a vector, `V`,
`theta` is the angle between `A` and `B`,
and `n` is a unit length vector perpendicular to the plane containing `A` and `B`

The Dot Product is a scalar
If A and B are vectors such that
`A = < a_1,a_2,...,a_k>`
and
`B= < b_1,b_2,...,b_k>`

then
`A*B = sum_(i=1)^(k)(a_ixxb_i)`

it can also be evaluated as
`A*B = |\|A|\|xx|\|B|\|*cos(theta)`
where `theta` is the angle between A and B.

Answer 2

Work is a dot product.
It is given as:
`W=vecF*vecs`
Where:
`vecF` is a force (vector)
`vecs` is the displacement (vector)
The result is a SCALAR (basically a quantity without vectorial characteristics) and is measured in Joules (J).
To evaluate it you do:
`W=|vecF|*|vecs|*cos(theta)`
where you multiply the modulus of your vectors times the cosine of the angle between them.
For example:

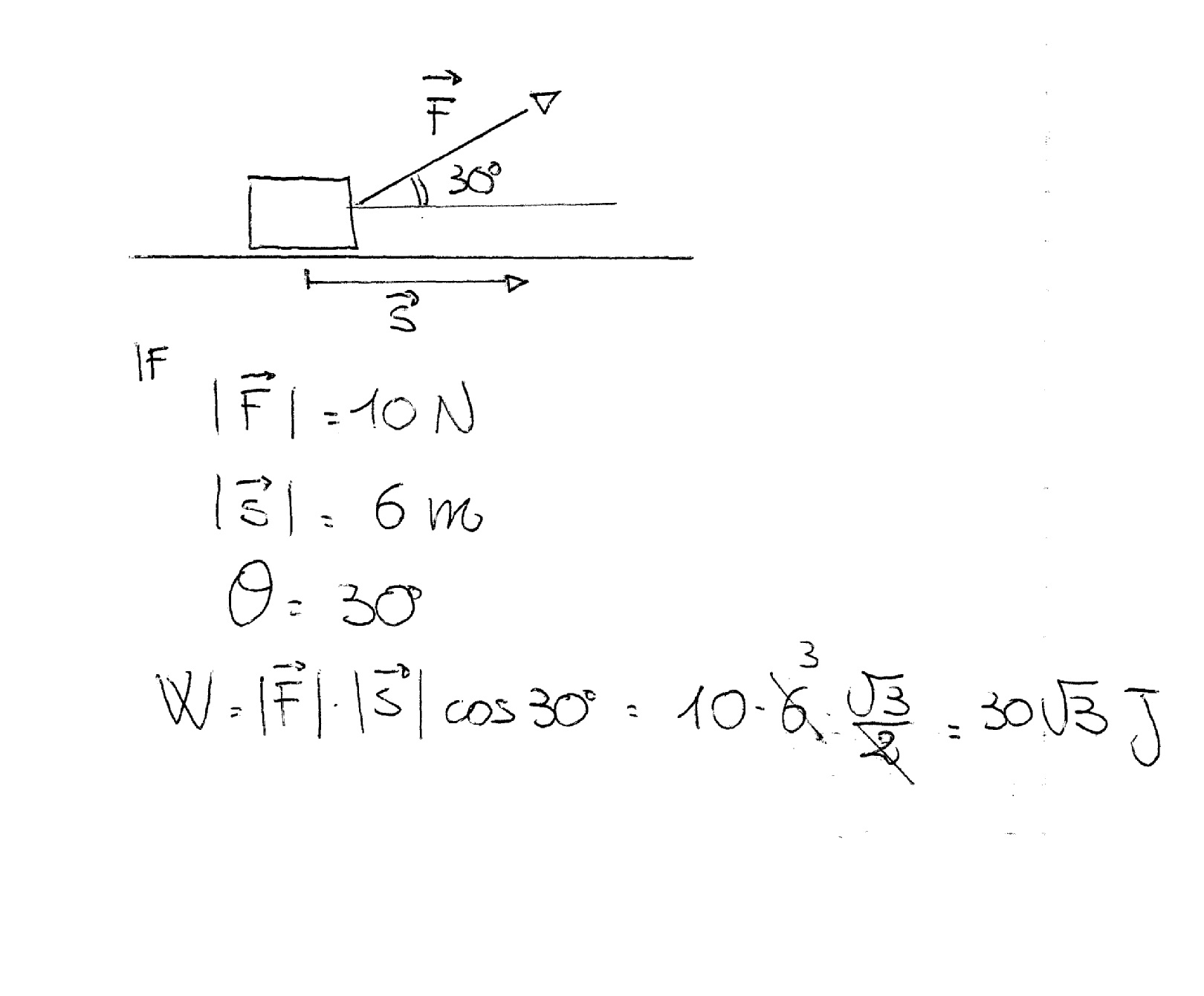
Hope it helps.