The inscribed cylinder's volume will be maximized when its radius is r=10/3 units and its height is 2 units.
Let r be the radius of the cylinder inscribed in the cone and let y be the cylinder's height. The volume of the cylinder is,
V=B*h=(\pi r^2)*y
Place an edge of the cone at the origin and take the x to be the distance to the edge of the inscribed cylinder from the outside of the cone. The diagram below shows x.
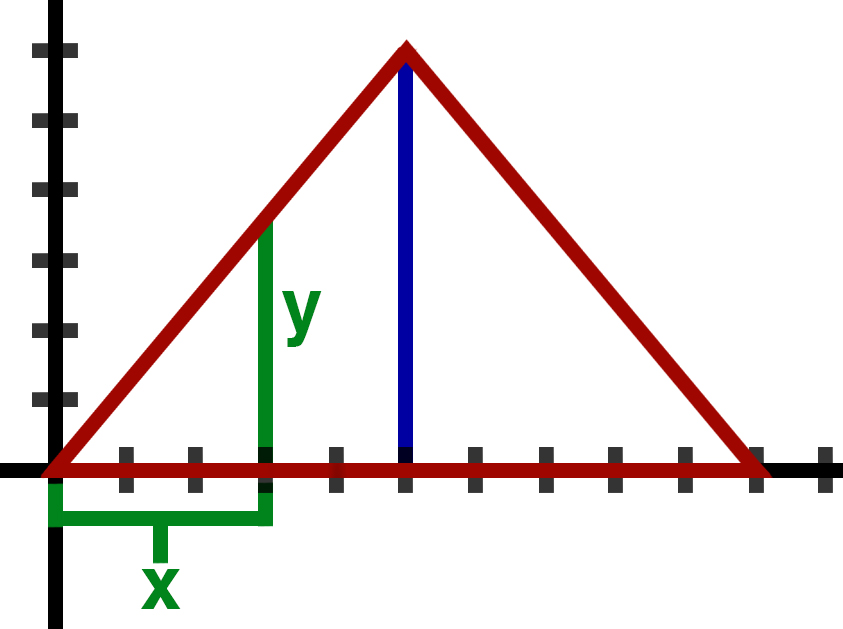
From the diagram, the radius of the inscribed cylinder is r=5-x. We can also express the height of the cylinder, y, in terms of x because we know the slope of the slanted side of the cone. For every five units we move to the right we go up 6 units.
Slope= {rise}/{run}=6/5
\implies y=6/5x
Substitute r and y into the top expression for V
V=\pi(5-x)^2*6/5x=6/5pi(x^3-10x^2+25x)
To find the maximum value of V, find when d/{dx}V=0.
Keep in mind that 0\leq x \leq 5 so that the left edge of the inscribed cylinder stays properly within the cone.
d/{dx}V=6/5pi(3x^2-20x+25)=0
\implies3x^2-20x+25=0
Use the quadratic formula to find x
x={20\pm\sqrt{400-4*3*25}}/{2*3}={20\pm10}/6
The answer between 0 and 5 is x=5/3
You can verify that x=5/3 gives the point of a maximum by graphing V in terms of x.
At x=5/3,,,,, y=6/5x=2 and r=5-x=10/3

