Final Answer: dy/dx={-x^2}/{1+x^2}dydx=−x21+x2
Let z =(x+y)z=(x+y)
tan(x+y)=x \quad \rarr \quad tan(z)=x
Take the derivative of each side with respect to x
d/dx[tan(z)]=d/dx[x]
sec^2(z)dz/dx=1 \quad \larr \quad \text{(Chain Rule)}
Now find what dz/dx is
dz/dx=d/dx[x+y]=d/dx[x]+d/dx[y]=1+dy/dx
substitute z and dz/dx into: \quad sec^2(z)dz/dx=1 and get
sec^2(x+y)(1+dy/dx)=1
Solve for dy/dx
dy/dx=cos^2(x+y)-1=-sin^2(x+y)
I used the trig identity: cos^2(z)-1=-sin^2(z) in the last step.
Substitute y to get the answer purely in terms of x
tan(x+y)=x \quad \rarr \quad y=arctan(x)-x
dy/dx=-sin^2(arctan(x))
Answer can be simplified with some work
Let theta=arctan(x) \implies tan(theta)=x/1=\text{opposite}/\text{adjacent}
The above expression implies the triangle below
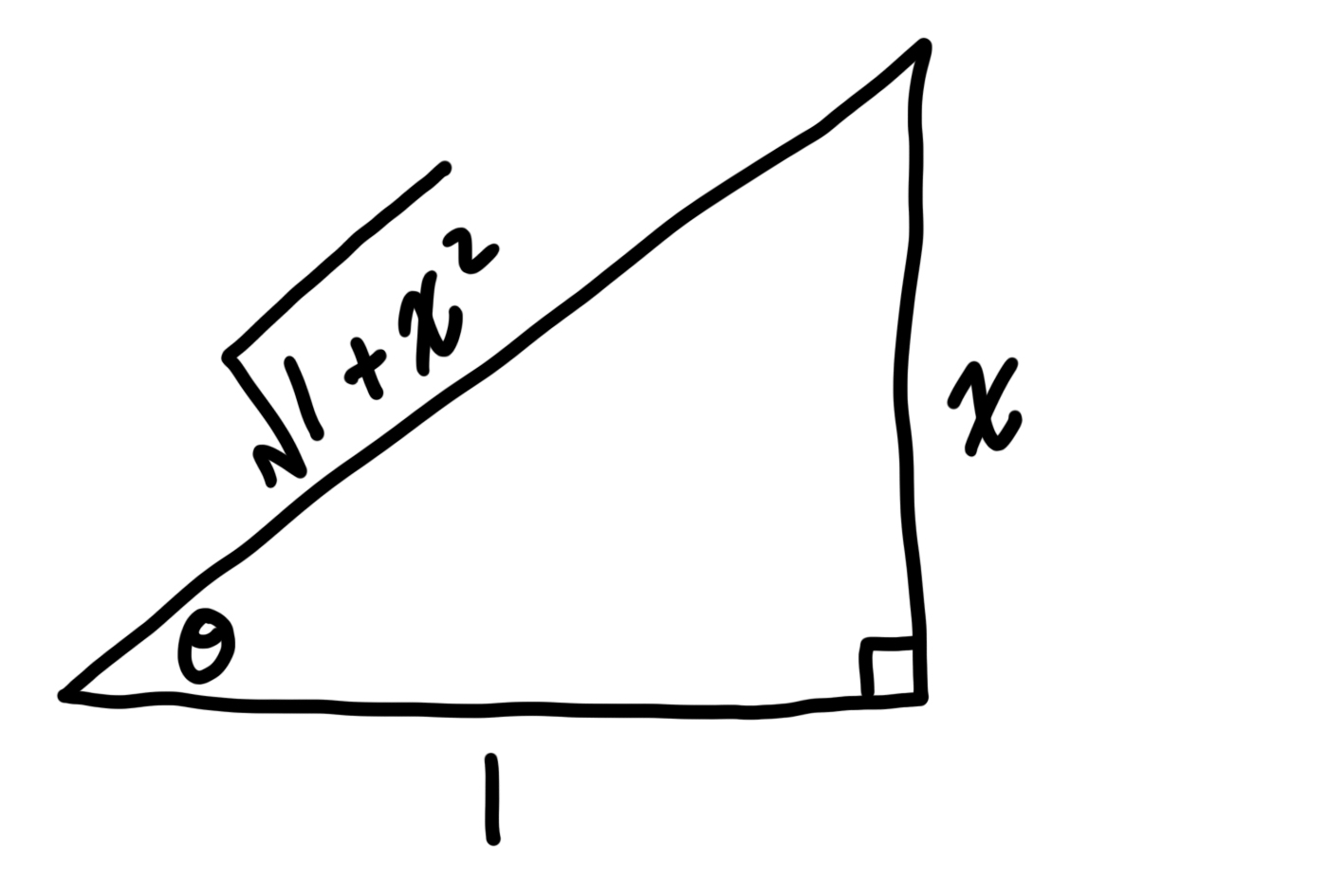
Sub arctan(x)=theta into the dy/dx expression
dy/dx=-sin^2(theta)=-(\text{opposite}/\text{hypotenuse})^2
From the diagram we know sin(theta)=x/\sqrt{1+x^2}. So...
dy/dx={-x^2}/{1+x^2}

