A farmer owns 1000 meters of fence, and wants to enclose the largest possible rectangular area. The region to be fenced has a straight canal on one side, and thus needs to be fenced on only three sides. What is the largest area she can enclose?
1 Answer
Jun 20, 2015
I found:
Explanation:
Considering the field as:
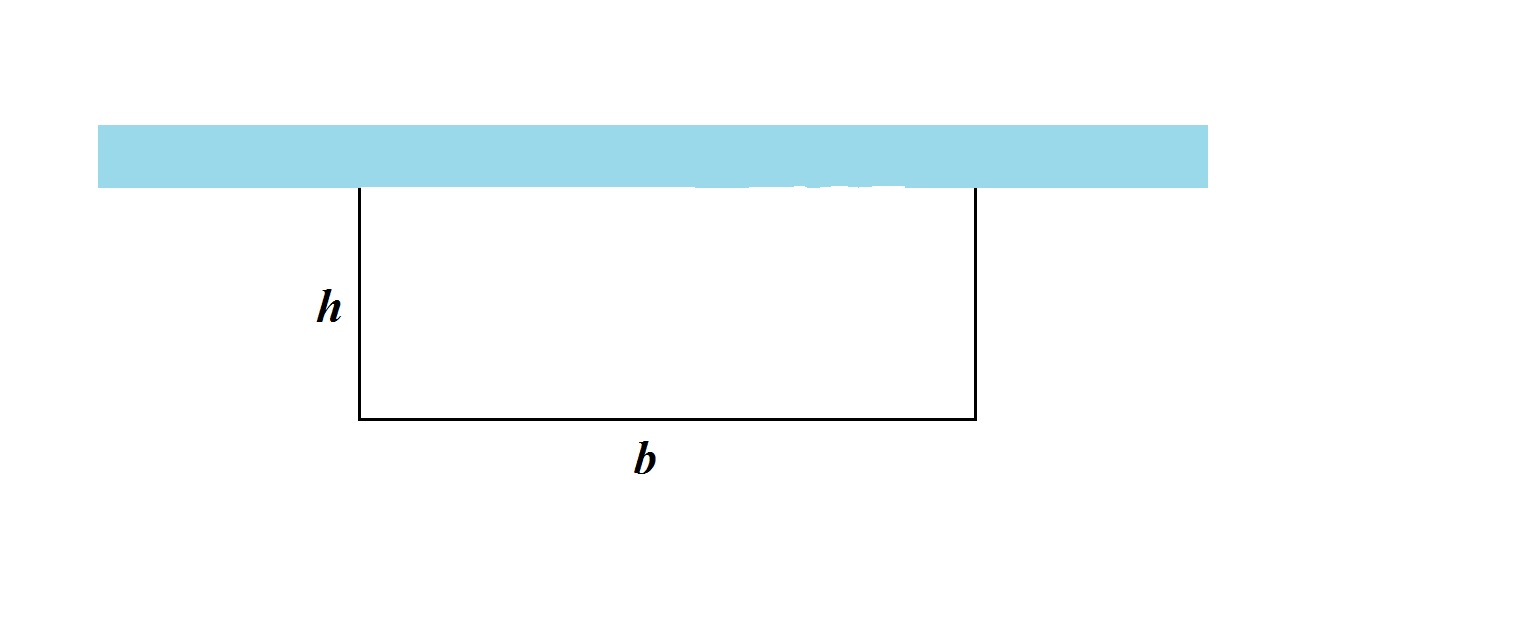
I know that the perimiter (only on 3 sides) to be fenced is equal to the meters of fence at disposal of the farmer:
The area will be
From (1)
Derive
equal it to zero to maximize it:
use this back in (1) you find
Use these dimensions in (2):

