Question

Question #65437

Answer 1

QUANTUM NUMBERS

The three main quantum numbers describe the shape, energy level, and orientation of the atomic orbitals.

There is a fourth (`m_s`) which describes the spin of an electron in an orbital, and it is purely based on the properties of the electron.

• `n` is the principal quantum number which describes the energy level.

`n = 1, 2, 3, . . .` and is always a positive integer.

• `l` is the orbital angular momentum quantum number which describes the shape of the orbital. `l = 0, 1, 2, 3, . . . , n-1`.

`l = 0, 1, 2, 3, ...` for `s, p, d, f, ...` orbitals, respectively.

• `m` (more specifically, `m_l`) is the magnetic quantum number, which corresponds to each unique orbital orientation. `m_l` takes on the set of integers from `-l` to `l`, i.e.

`m_l = {0, pm1, pm2, . . . , pml}`.

• `m_s` (see why we need to say `m_l`?) is the electron spin quantum number, which describes the spin of the electron. It is only `pm1/2`, independent of the other quantum numbers.

2P ATOMIC ORBITAL

For example, a `2p` orbital is said to have:

• `n = 2` since it's `color(highlight)(2)p`
• `l = 1` since it's `2color(highlight)(p)`
• `m_l = {0, pm1, . . . , pm l} = {-1, 0, +1}`
  (if `l = 2`, then `m_l = {-2, -1, 0, +1, +2}`)

If the orbital has an electron, the electron's `m_s` is either `+"1/2"` or `-"1/2"` for spin up and spin down, respectively. Technically, we just say `pm"1/2"` because it could take either configuration (neither is preferential over the other).

We cannot say which electron is which, because they are indistinguishable.

The `2p_z` orbital looks like this:

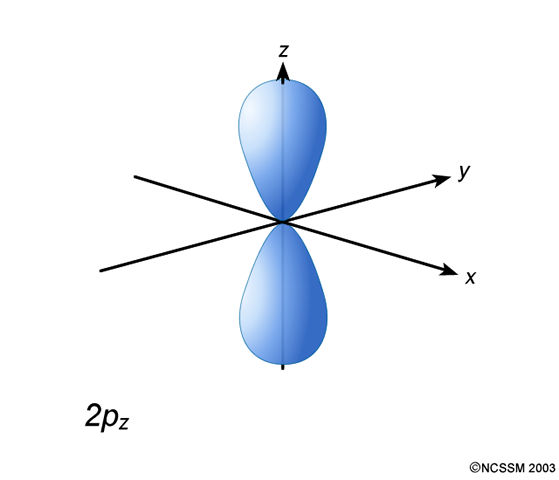
• While `m_l = 0`, that corresponds to the `2p_z` orbital.
• While `m_l = -1`, that corresponds to the `2p_x` or `2p_y` orbital.
• While `m_l = +1`, that corresponds to the `2p_y` or `2p_x` orbital. (The uniqueness that `m_l = pm1` matters, but the choice of assigning either to `p_x` or `p_y` is arbitrary.)

Lastly, the observations you learn from General Chemistry describe the idea that electrons fill the orbitals:

• with the lowest energy first, in part due to `n` (Aufbau Principle)
• one at a time
• in such a way that `m_s` is not the same for any two electrons both in a doubly-occupied orbital (Pauli Exclusion Principle).