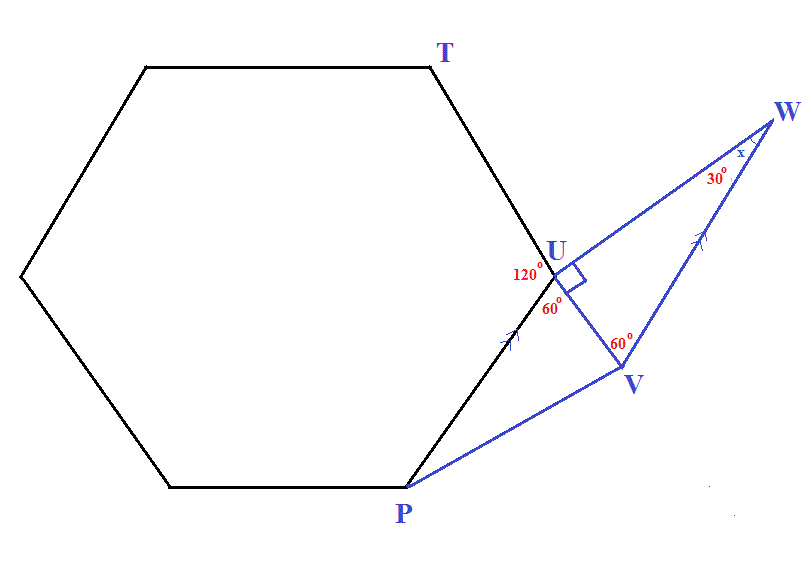
Here's how the image looks like
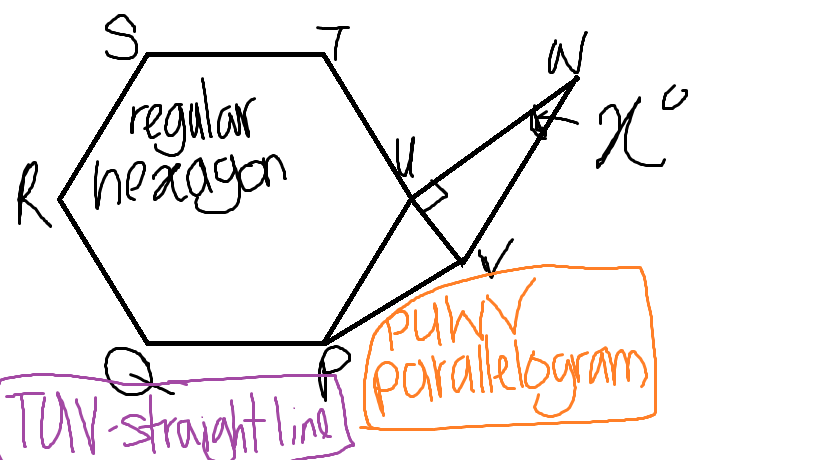
The first important thing you need to notice is that you're dealing with a regular hexagon, which means that all the interior angles are equal to #120""^@#.
So, if #angle(TUP)# is equal to #120""^@# and #TUV# is a straight line, then angle #angle(PUV)# is its complementary angle.
This means that
#angle(TUP) + angle(PUV) = 180""^@#
As a result,
#angle(PUV) = 180 - 120 = 60""^@#
Now, #triangleVUW# is a right triangle, as you can deduce from the fact that #angle(VUW)# is equal to #90^""@#.
Another important thing to notrice here is that #PUWV# is a parallelogram, which means that #bar(UN)# is parralel to #bar(WV)#
If this is the case, then #angle(PVU)# is equal to #90""^@# as well, since you're dealing with two parallel lines intersected by a straight line.
Moreover, #angle(PUV)# is equal to #angle(UVW)# for the same reason.
This means that
#angle(UVW) = angle(PUV) = 60""^@#
Therefore, #angle(VWU)# (angle #x#) will be
#angle(VWU) + angle(VUW) + angle(UVW) = 180""^@#
#angle(VWU) = 180 - 90 - 60 = color(green)(30""^@)#