Question

How do use the first derivative test to determine the local extrema `f(x)=x^4-4x^3+4x^2+6`?

Answer 1

You get: 2 minima and 1 maximum.

Explanation:

We can study the derivative of the function:
`f'(x)=4x^3-12x^2+8x`
Set the derivative equal to zero:
`f'(x)=0`
`4x^3-12x^2+8x=0`
`4x(x^2-3x+2)=0`
With solutions:
`x_1=0`
`x^2-3x+2=0` using the Quadratic Formula:
`x_(2,3)=(3+-sqrt(9-8))/2=(3+-1)/2`
two solutions:
`x_2=2`
`x_3=1`
We can now study the sign of the derivative setting: `f'(x)>0` getting:

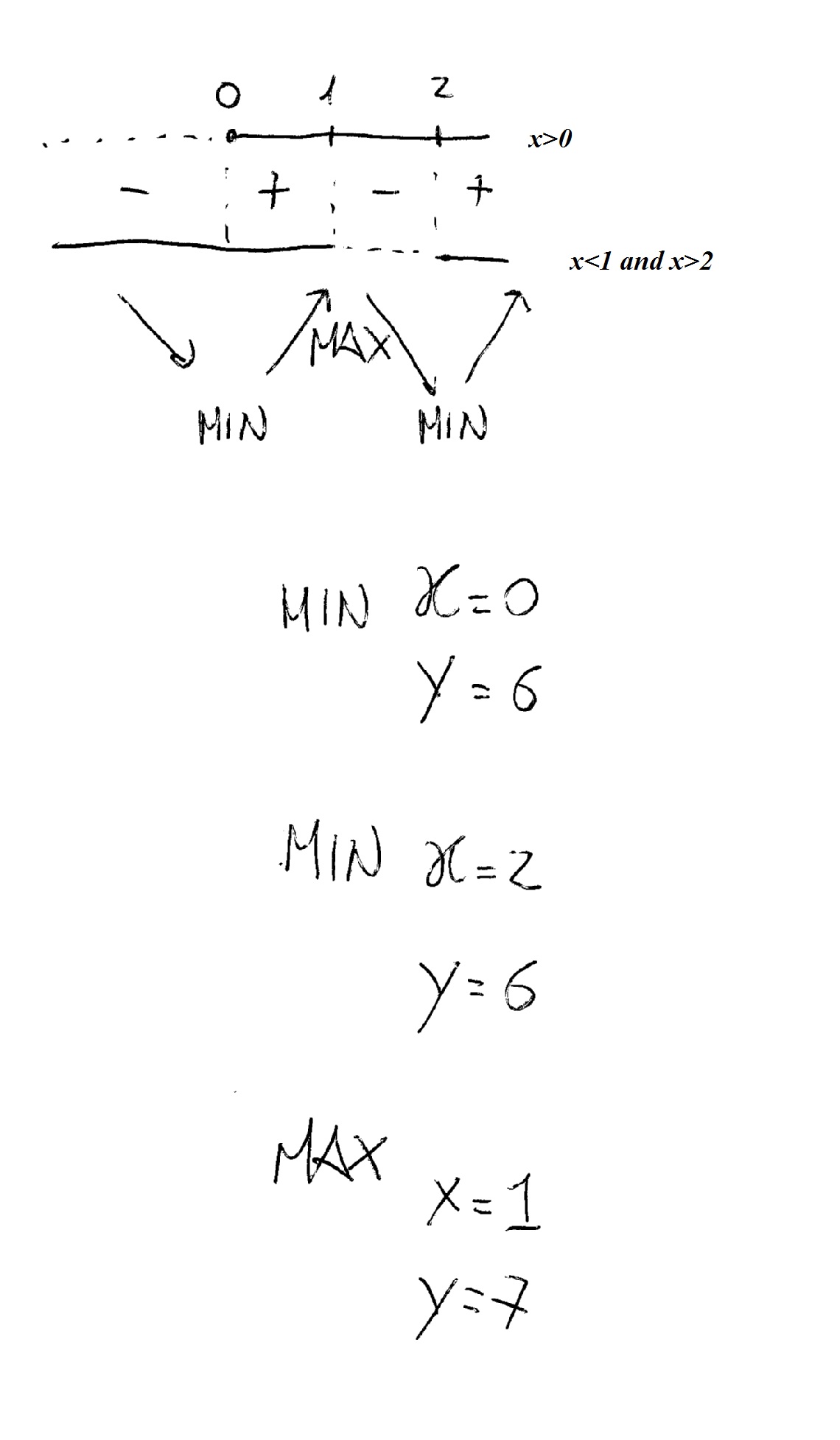
Graphically:
graph{x^4-4x^3+4x^2+6 [-20.27, 20.28, -10.14, 10.13]}