Question

How do you find the 6 trigonometric functions for 0 degrees?

Answer 1

`sin(0^o) = 0color(white)("XXXX")csc(0^o) "undefined"`
`cos(0^o)=1color(white)("XXXX")sec(0^o)=1`
`tan(0^o)=0color(white)("XXXX")cot(0^o) "undefined"`

Explanation:

Using a triangle in standard position with the angle involved at the origin,
the 6 basic trigonometric functions are defined as

`sin = "opposite"/"hypotenuse"color(white)("XXXX")csc ="hypotenuse"/"opposite"`

`cos = "adjacent"/"hypotenuse"color(white)("XXXX")sec ="hypotenuse"/"adjacent"`

`tan = "opposite"/"adjacent"color(white)("XXXX")cot="adjacent"/"opposite"`

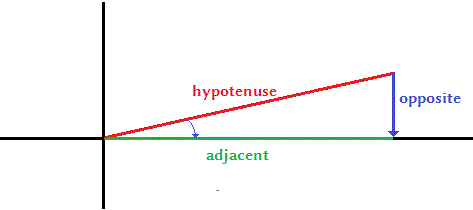
From the above image we can see that as the angle approaches `0`

• the length of the opposite side also approaches `0` and

• the length of the hypotenuse and the length of the adjacent side become equal.

This gives the values as in the "Answer" for the 6 basic trig functions.