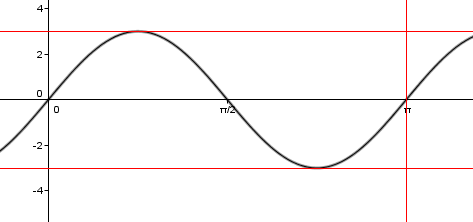
The general form for a sin function is;
y=Asin(Bx + C) +D
Each constant, A, B, C, and D tells us something about the function. C and D tell us the horizontal and vertical shift of the function. In the case of y=3sin(2x) both are zero, so the graph isn't translated up or to the side.
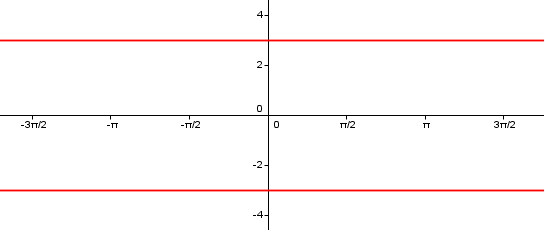
A is the amplitude, so A=3 tells us that the graph is going to fluctuate between 3 and -3.
Lastly, B is the frequency. B=2 tells us that there will be 2 full waves between 0 and 2pi. A more useful number would be the period, p.
p = (2pi)/B = (cancel(2)pi)/cancel(2) = pi
So we know that the wave is going to repeat every pi radians.
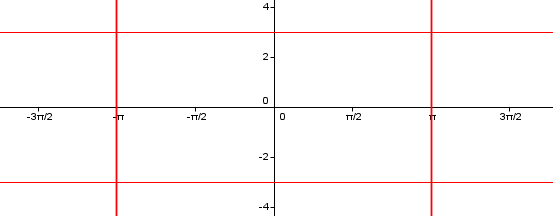
A sin wave starts at 0, goes to A, back to 0, then to -A.