How do you find the exact functional value sin 11/12 pi using the cosine sum or difference identity?
1 Answer
Aug 27, 2015
Explanation:
There are several different ways to answer this question.
I will arbitrarily use
∴
The sine sum identity is:
∴
We can use the unit circle to work out the values.
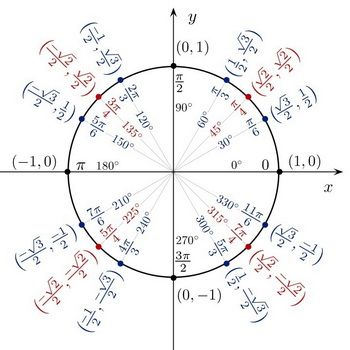
(from www.algebra.com)

