Two sides of a triangle are 6 m and 7 m in length and the angle between them is increasing at a rate of 0.07 rad/s. How do you find the rate at which the area of the triangle is increasing when the angle between the sides of fixed length is pi/3?
1 Answer
The overall steps are:
- Draw a triangle consistent with the given information, labeling relevant information
- Determine which formulas make sense in the situation (Area of entire triangle based on two fixed-length sides, and trig relationships of right triangles for the variable height)
- Relate any unknown variables (height) back to the variable
#(theta)# which corresponds to the only given rate#((d theta)/(dt))# - Do some substitutions into a "main" formula (the area formula) so that you can anticipate using the given rate
- Differentiate and use the given rate to find the rate you are aiming for
#((dA)/(dt))#
Let's write down the information given formally:
#(d theta)/(dt) = "0.07 rad/s"#
Then you have two fixed-length sides and an angle between them. The third length is a variable value, but it is technically an irrelevant length. What we want is
A theoretically consistent triangle is:
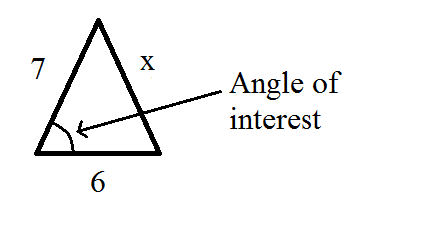
Keep in mind that this is not proportionally representative of the true triangle. The area of this can be found most easily with:
#A = (B*h)/2#
where our base is of course
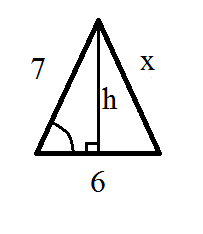
Now we do have a right triangle. Notice, however, that our area formula has
#sintheta = h/7#
#7sintheta = h#
So far, we have:
#(d theta)/(dt) = "0.07 rad/s"# (1)
#A = (Bh)/2# (2)
#7sintheta = color(green)(h)# (3)
So, we can plug (3) into (2), differentiate (2) and implicitly acquire
#A = (6*color(green)(7sintheta))/2 = 21sintheta#
#color(blue)((dA)/(dt)) = 21costheta((d theta)/(dt))#
#= 21costheta ("0.07 rad/s")#
Finally, at
#= 10.5(0.07) = color(blue)("0.735 u"^2"/s")#
(note that

