Question

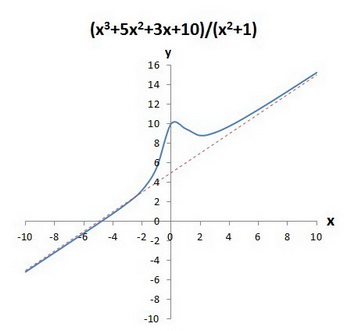
What is the oblique asymptote of `y = ( x^3 + 5x^2 + 3x + 10 )/( x^2 + 1 )`?

Answer 1

The oblique asymptote is `color(red)(y = x +5)`

Explanation:

`y = (x^3+5x^2+3x+10)/(x^2+1)`

A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.

To find the slant asymptote you must divide the numerator by the denominator.

I will use synthetic division:

`" "" "|1" "5" "3" "10`
`color(white)(1)-1|" "color(white)(1)-1color(white)(1)-5`
`0" "color(white)(1)|" "0" "0`
`" "" "stackrel("—————————)`
`" "" "color(white)(1)1" "5" "color(red)(2" "color(white)(1)5)`

The quotient is `x+5` with a remainder of `2x+5`.

We can ignore the remainder, so the oblique asymptote is `y=x+5`.