Question

How do you long divide `(x^3 + x^2 - x - 1) div(x - 1)`?

Answer 1

`(x^3+x^2-x-1)/(x-1) = x^2+2x+1`

Explanation:

Long dividing polynomials is similar to long dividing integers...

Write the dividend under the bar and the divisor to the left.

Choose the first term of the quotient so that when multiplied by the divisor it matches the leading term of the dividend. In our case, we write `x^2` above the bar as the first term, since `(x-1) * x^2 = x^3-x^2`, matching the leading term `x^3`.

Write this product under the dividend and subtract it to give a remainder `2x^2`. Bring down the next term `-x` of the dividend alongside it.

Choose the next term of the quotient so that when multiplied by the divisor it matches the leading term in the remainder. In our case, we write `+2x` above the bar, since `(x-1) * 2x = 2x^2-2x`, matching the leading term `2x^2`.

Write this product under the remainder and subtract it to give a remainder `x`. Bring down the next term `-1` of the dividend alongside it.

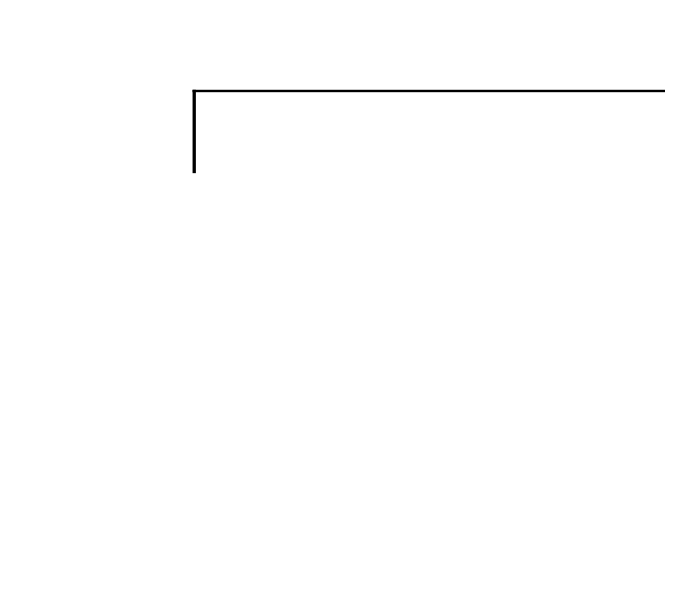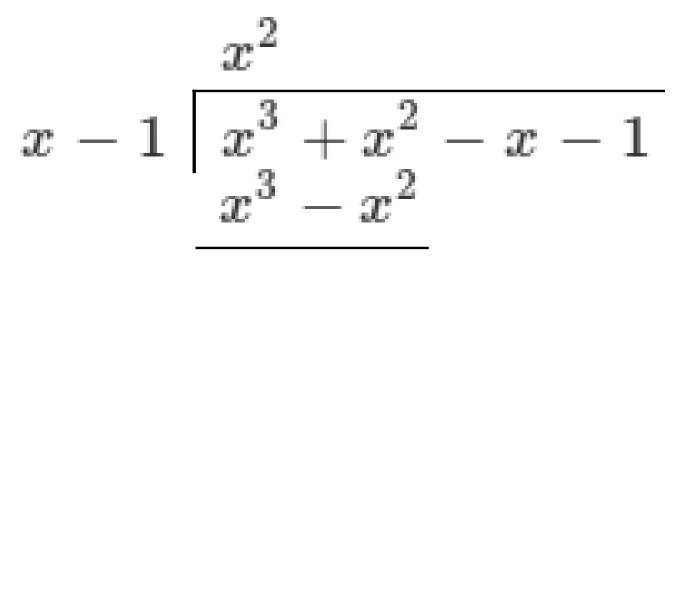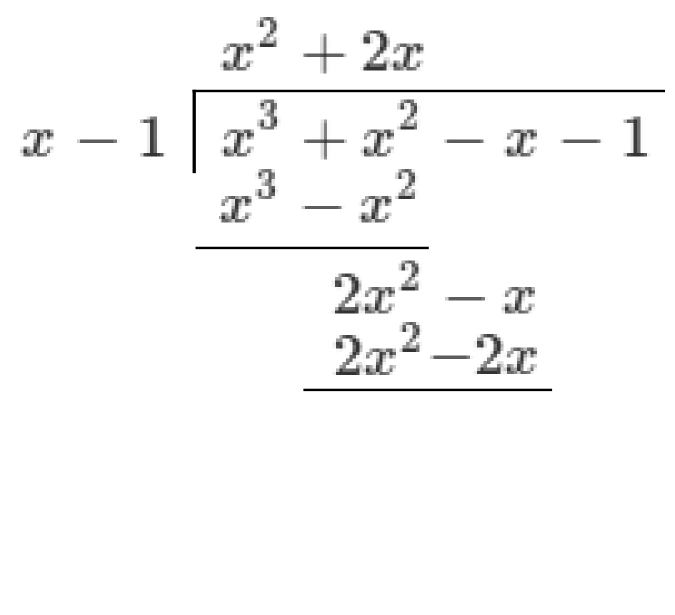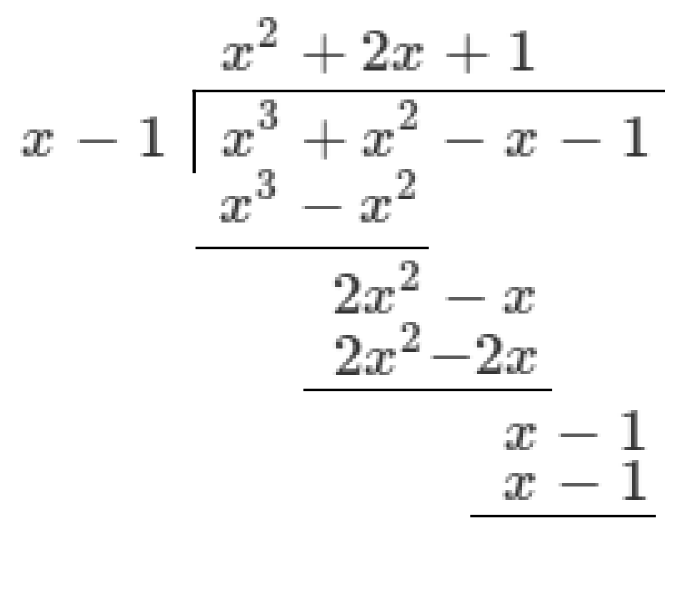
Choose the final term of the quotient so that when multiplied by the divisor it matches the leading term in the remainder. In our case, we write `+1` above the bar, since `(x-1) * 1 = x - 1`, matching the leading term `x`.

Write this product under the remainder and subtract it. No remainder is left and there are no more terms in the divisor to bring down, so we're done.

In this case the division was exact. In general, you may be left with a remainder at the end.