How would I be able to figure out the reference angle in radians of #(5pi)/6#?
1 Answer
Sep 25, 2015
Explanation:
The definition of the reference angle, is that it's the smallest angle that's made using the x-axis at reference while having the same coordinates at the unit circle.
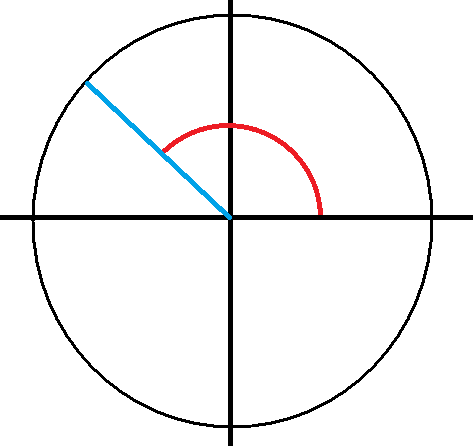
Now, the angle in red is
So that's your reference angle.

