What is a possible set of four quantum numbers (n,l ,ml ,ms ) for the highest-energy electron in Ga?
1 Answer
Here's what I got.
Explanation:
Your starting point here will be gallium's electron configuration.
Gallium,
The electron configuration of gallium looks like this - I'll use the noble gas shorthand notation
#"Ga: " ["Ar"]3d^10 4s^2 4p^1#
Now, you're interested in finding the possible sets of quantum numbers that describe the highest-energy electron that belongs to a gallium atom.
As you know, the quantum numbers are defined
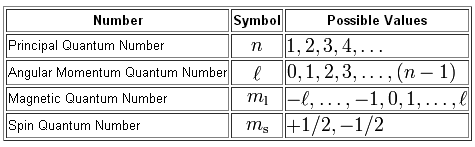
So, the highest-energy electron found in gallium is located in a 4p-orbital, which means that right from the start you know that the value of its principal quantum number,
Now for the angular momentum quantum number,
Notice that the fourth energy level has total of
#l =0 -># the s-subhell#l = 1 -># the p-subshell#l=2 -># the d-subshell#l=3 -># the f-subshell
SInce your electron is located in the p-subshell, it follows that its
The magnetic quantum number,
For the p-subshell,
#m_l = -1 -># the#p_x# orbital#m_l = color(white)(-)0 -># the#p_y# orbital#m_l = color(white)(-)1 -># the#p_z# orbital
Since the p-subshell only contains one electron, you can place it in the first available p-orbital, which is
Finally, the spin quantum number,
#m_s = -1/2 -># a spin-down electron#m_s = +1/2 -># a spin-up electron
Since the orbital only contains one electron, it follows that it could be either spin-up or spin-down, so you get two possible sets of quantum numbers
#n=4 -> l=1 -> m_; = -1 -> m_2 = -1/2#
A spin-down electron located in the
#n=4 -> l=1 -> m_; = -1 -> m_2 = +1/2#
A spin-up electron located in the

