Question

How do you verify `(cos(x))(cos(x)) = 1-sin^2(x)`?

Answer 1

We can rewrite the equation as `cos^2(x)=1-sin^2(x)`, and thus as

`cos^2(x)+sin^2(x)=1`

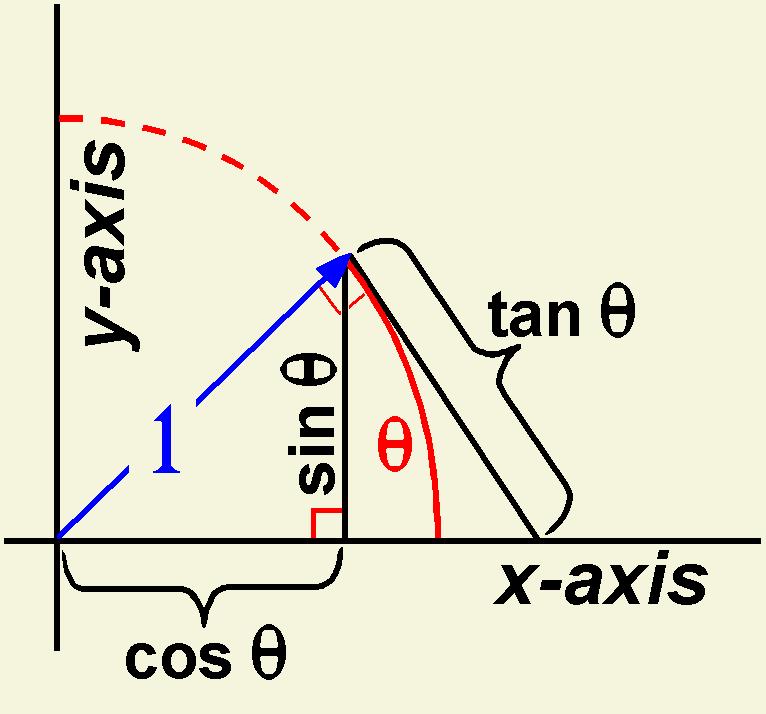
This is a fundamental equality for the trigonometric function, and its explanation is very simple: if you consider the unit circle, any point on the circumference `(x,y)` is of the form `(cos(alpha), sin(alpha)`, for some angle `alpha` which identifies the point.

Since `cos(alpha)` is the `x` coordinate and `sin(alpha)` is the `y` coordinate of the point, we have that `cos(alpha)` and `sin(alpha)` are the catheti of a right triangle, whose hypotenusa is the radius, which is one. So, we have that

`cos^2(alpha)+sin^2(alpha) = 1^2 = 1`

I hope this image can help, since it shows that the sine and cosine of an angle form a right triangle whose hypotenusa is the radius.