Question

Among all right circular cones with a slant height of 12, what are the dimensions (radius and height) that maximize the volume of the cone?

Answer 1

The volume of a right circular cone using slant height `l` is...

`V=(1/3)pir^2sqrt(l^2-r^2)`

Explanation:

Plugging in the slant height of 12 into the volume equation:

`V=(1/3)pir^2sqrt(12^2-r^2)`

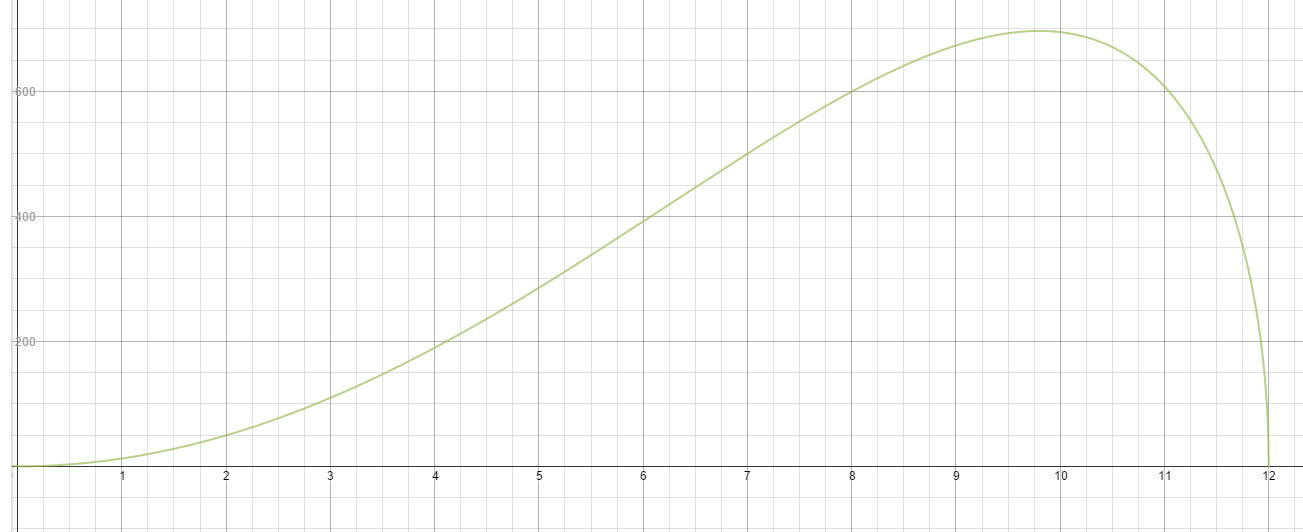
A graph of the volume function is shown below.

Next, take the derivative with respect to r:

`(dV)/(dr)= -(pi r (r^2-96))/sqrt(144-r^2)`

Now, find the maximum by setting the above derivative equal to zero and solving for r:

Since r must be a positive number , the only valid solution is:

`r=sqrt96=4sqrt6`

Verify this is a maximum by checking the first derivative near this solution. To the left, V' is positive and to the right it is negative indicating this is indeed a Maximum.

Finally, the height is ...

`h=sqrt(144-r^2)=sqrt(144-96)=sqrt48=4sqrt3`

hope that helps