How do you calculate how many stereoisomers a compound has?
1 Answer
Since for every atom that can exist in more than one configuration, you have R or S (
- If you had
#2# of those atoms, then you have#4# configuration combinations: (R,R), (R,S), (S,R), (S,S). - For
#3# of those atoms, you have: (R,R,R), (R,R,S), (R,S,R), (S,R,R), (R,S,S), (S,R,S), (S,S,R), (S,S,S), which is#8# .
Let us call an atom or group of atoms that can exist in more than one configuration a stereounit.
That means for
However, note that if there are any meso compounds (i.e. if the molecule has a chance of having a plane of symmetry dividing two identical halves that each contain asymmetric centers), then we must account for them because the symmetry reduces the number of different compounds.
An example of a meso compound vs. a regular chiral compound...
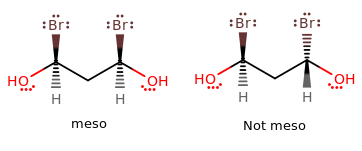
Thus, we revise the formula to give:
#\mathbf("Total Stereoisomers" = 2^n - "meso structures")# where
#n = "number of stereounits"# .
Note that if we had used the traditional definition of a stereocenter instead of a stereounit (i.e.
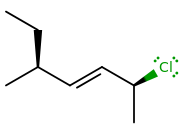
...it has two stereocenters, but three atoms which can be in more than one configuration.
Hence, by the stereocenter definition, it has 4 structures, when in fact it DOESN'T.
Two configurations for the left carbon, two configurations for the right carbon, and two configurations for the middle carbon, meaning

