By the five-point method, you need five points to graph the function, #f(x)=4sin(x-pi/2)#. To find the five points, first find the five points for its parent function #e(x)=sinx#. Ignore the negative x values and its corresponding y values in the table below.
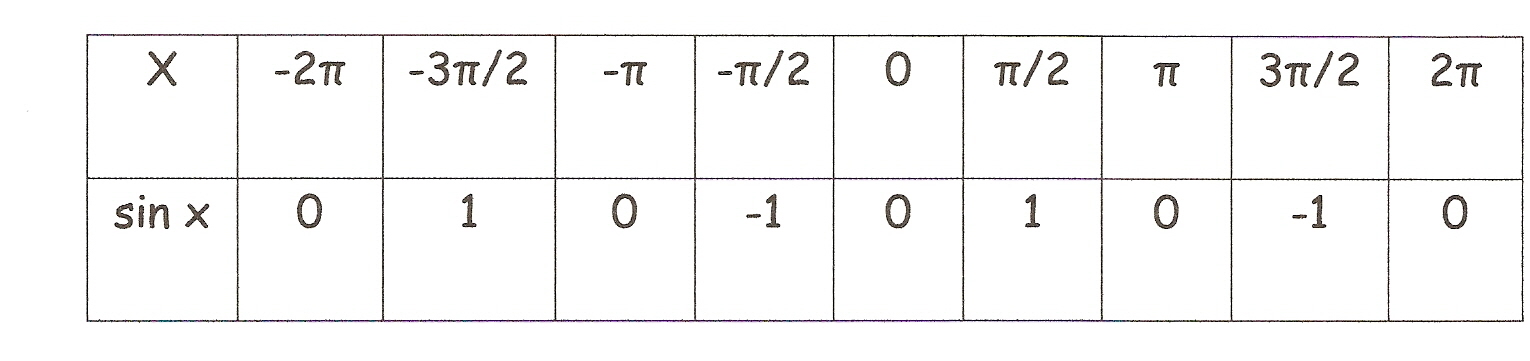
Now that you have the five points for the parent function, use the mapping rule to apply transformations in order to find the five points for the transformed function, #f(x)=4sin(x-pi/2)#.
Mapping rule: #(x+color(red)(pi/2),color(blue)4y)#
#f(x)=4sin(x-pi/2)#
Point #1. (0+color(red)(pi/2), color(white)(xxx)(color(blue)4)0) rArr color(white)(xxxxxxxxx)(pi/2,0)#
Point #2. (pi/2+color(red)(pi/2), color(white)(xx)(color(blue)4)1) rArr color(white)(xxxxxxxxx)(pi,4)#
Point #3. (pi+color(red)(pi/2), color(white)(xxx)(color(blue)4)0) rArr color(white)(axxxxxxxx)((3pi)/2,0)#
Point #4. ((3pi)/2+color(red)(pi/2), color(white)(ix)(color(blue)4)(-1)) rArr color(white)(xxxxxx)(2pi,-4)#
Point #5. (2pi+color(red)(pi/2), color(white)(xx)(color(blue)4)0) rArr color(white)(xxxxxxxxx)((5pi)/2,0)#
The transformed graph would look like:
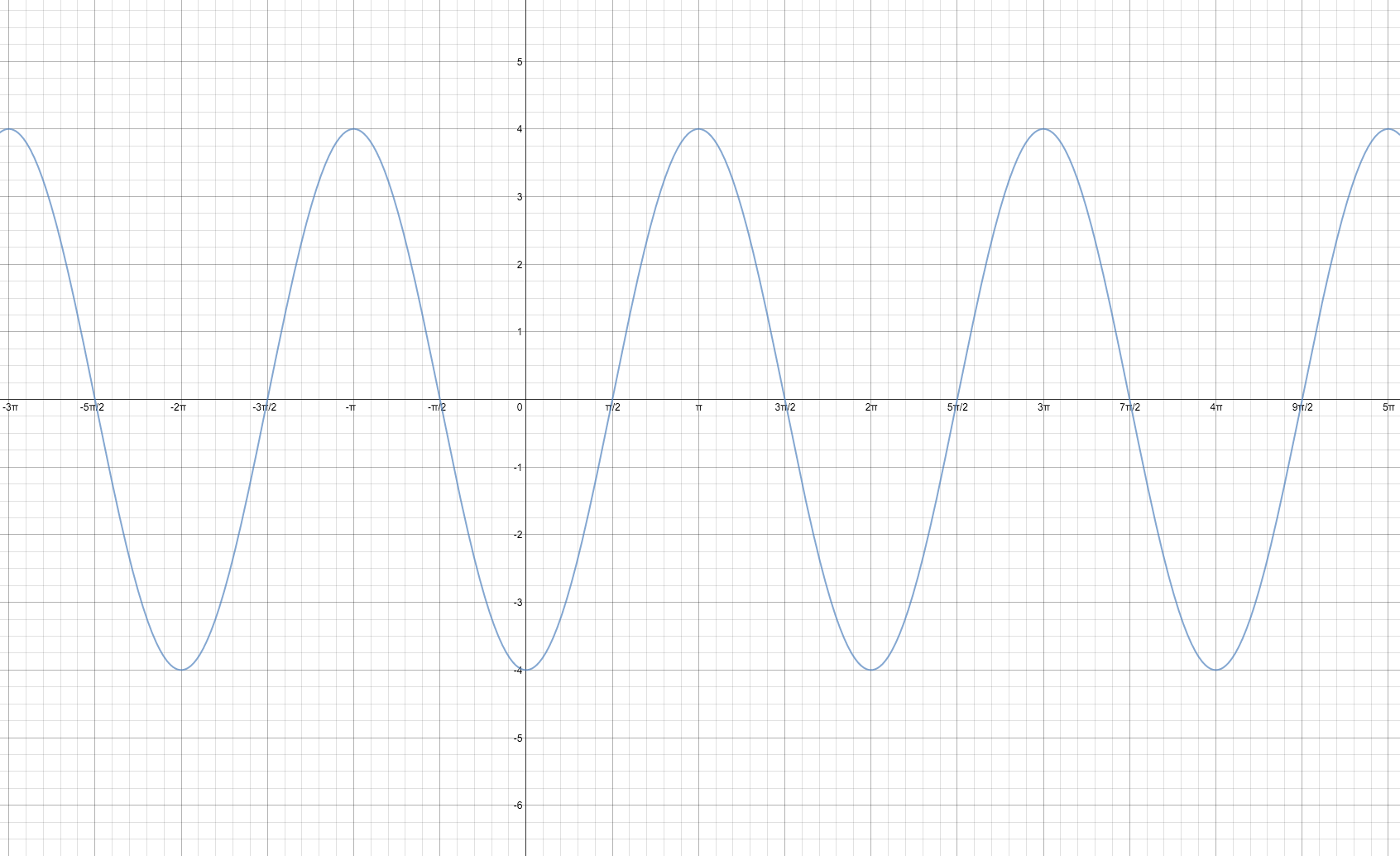
Zoom in to check the five main points shown on the graph.



