Question #03abb
2 Answers
Explanation:
The trick is to nearly always draw a diagram and this will help the understanding of what is going on.
Given that:
and that PC = 2 units marries up very well with triangle PBC. This shows that this diagram is correct.
PC is parallel to AQ so
Thus
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using Pythagoras and the given of:
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Thus
We are asked to find:
From the diagram:
The answer is (4)
Explanation:
The idea here is that you need to draw the
Now, you are told that an angle of
#color(red)(alpha) = tan^(-1)(sqrt(3)/2)#
exists between the resultant, which we'll call
#tan(color(red)(alpha)) = [tan^(1-)(sqrt(3)/2)] = sqrt(3)/2#
Keep this in mind. Now, here's a very rough sketch of the two forces
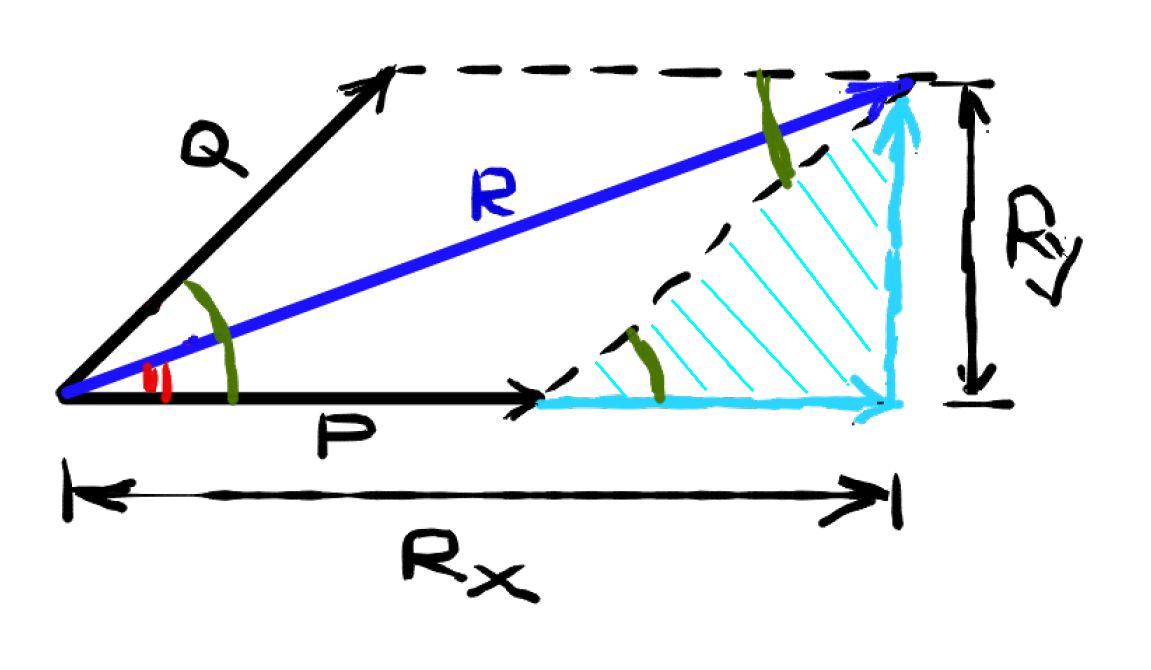
So,
The resultant,
The idea here is that you need to write
Now, focus on the triangle marked with light blue lines. Using the angle
#R_y = Q * sin(color(green)(beta))#
Here
At the same time, you can say that the leg of this triangle located on the
#R_x = P + Q * cos(color(green)(beta))#
Use the given
#{(R_y = 2P * sin(color(green)(beta))), (R_y = P + 2P * cos(color(green)(beta))) :}#
Finally, focus on the triangle formed by the two projections of the resultant ans the resultant. You know that
#tan(color(red)(alpha)) = sqrt(3)/2#
At the same time,
#tan(color(red)(alpha)) = R_y/R_x#
This means that you have
#sqrt(3)/2 = (2 color(red)(cancel(color(black)(P))) * sin(color(green)(beta)))/(color(red)(cancel(color(black)(P))) + 2color(red)(cancel(color(black)(P))) * cos(color(green)(beta)))#
#sqrt(3)/2 = (2sin(color(green)(beta)))/(1 + 2cos(color(green)(beta)))#
This is equivalent to
#sqrt(3) + 2sqrt(3) * cos(color(green)(beta)) = 4 * sin(color(green)(beta))#
Looking at the options given to you, the only one that matches this equation corresponds to
#sqrt(3) + 2sqrt(3) * cos(60^@) = 4 * sin(60^@)#
#sqrt(3) + color(red)(cancel(color(black)(2)))sqrt(3) * 1/color(red)(cancel(color(black)(2))) = 4 * sqrt(3)/2#
#2sqrt(3) = 2sqrt(3) color(white)(x)color(green)(sqrt())#


