What is the value of the hypotenuse of an isosceles triangle with a perimeter equal to 16 + 16sqrt2?
1 Answer
Jan 6, 2016
The final answer is
Explanation:
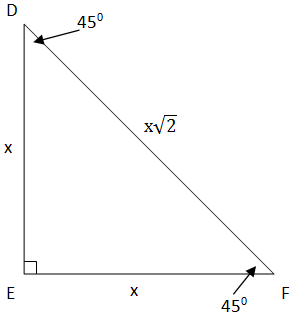 PlatinumGMAT, 2015
PlatinumGMAT, 2015
From the photo, we can see that the perimeter of an isosceles right triangle is
And since we're looking for the * hypotenuse

