The sail on a toy boat is in the shape of an isosceles triangle. Its legs are 12 inches long and its base angles measure 70°. How long to the nearest hundredth of an inch, is the base of the sail?

1 Answer
Johnson Z. · Alan P.
Jan 30, 2016

base#=8.20# #"inches"#

Explanation:

If we were to cut the whole isosceles triangle in half, two right triangles would be produced:
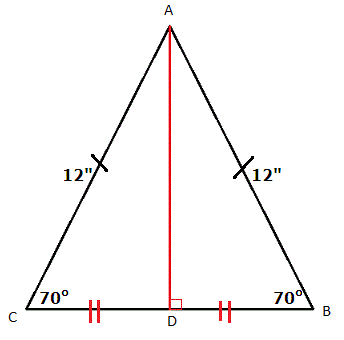
http://study.com/academy/lesson/what-is-an-isosceles-triangle-definition-properties-theorem.html (modified)

Using a primary trigonometric ratio , we can determine the base length of one of the right triangles. In this case, we can use cosine. Recall that:

#costheta="adjacent"/"hypotenuse"#

To find the base length, or the "adjacent," substitute your known values into the formula:

#costheta="adjacent"/"hypotenuse"#

#cos70^@="adjacent"/12#

#12(cos70^@)="adjacent"#

#"adjacent"~~4.10# #"inches"# #rArr# rounded off to two decimal places

Recall that the base length of the left triangle is equal to the base length of the right triangle. Thus, multiply #4.10# #"inches"# by #2# to get the base length of the whole isosceles triangle:

#4.10*2#
#~~8.20# #"inches"#

#:.#, the base length of the sail is approximately #8.20# #"inches"#.

Related questions
See all questions in Angles with Triangles and Polygons
Impact of this question
2353 views around the world
You can reuse this answer
Creative Commons License