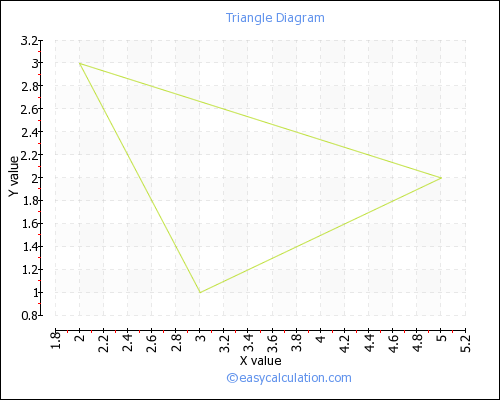
What is the centroid of a triangle with corners at #(3 , 1 )#, #(2 , 3 )#, and #(5 , 2 )#?

1 Answer
Johnson Z.
Feb 1, 2016

centroid#=(10/3,2)#

Explanation:

When graphed, the triangle would look like:

https://www.easycalculation.com/analytical/draw-triangle.php

By definition, the centroid is the point of intersection between the medians in a triangle. A median is a line segment from a corner of the triangle to the midpoint of its opposite side.

Recall that the formula for centroid is:

#C=((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)#

where:
#C=#centroid
#(x_1,y_1)=(3,1)#
#(x_2,y_2)=(2,3)#
#(x_3,y_3)=(5,2)#

To find the coordinates of the centroid, substitute your known points into the centroid formula:

#C=((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)#

#C=((3+2+5)/3,(1+3+2)/3)#

#C=(10/3,6/3)#

#C=(10/3,2)#

#:.#, the centroid is at #(10/3,2)#.

Related questions
See all questions in Medians and Centroids
Impact of this question
2756 views around the world
You can reuse this answer
Creative Commons License