For the angular distribution function #Y_(l)^(m_l)(theta,phi)#, #m_l# stands for the projection of the angular momentum #l#. As it turns out, it is basically the shape of the orbitals because it corresponds to the #z# angular momentum of the orbital.
THE MAGNETIC QUANTUM NUMBER, FOR THE 4F ORBITAL
#m_l#, the magnetic quantum number, takes on the values #0, pm1, pm2, . . . , pm l#, where #l# is an integer. For each #l#, there corresponds an orbital name, so #l = 0 -> s#, #l = 1 -> p#, #l = 2 -> d#, #l = 3 -> f#, #l = 4 -> g#, etc.
For the #4f# orbital, #n = 4# and #l = 3#, meaning that #m_l = 0, pm1, pm2, pm3#.
Therefore, there are #7# #m_l# values for the #4f# orbital, and there happens to be 7 different #4f# orbitals:
- #4f_(y(3x^2-y^2)): m_l = -3#
- #4f_(z(x^2-y^2)): m_l = -2#
- #4f_(yz^2): m_l = -1#
- #4f_(z^3): m_l = 0#
- #4f_(xz^2): m_l = +1#
- #4f_(xyz): m_l = +2#
- #4f_(x(x^2-3y^2)): m_l = +3#
But why are there #7#? Yes, #m_l# correlates with how there are #7#, but there are other reasons why there are #7# unique #f# orbitals.
MORE-OR-LESS WHY THERE ARE #\mathbf(2l+1)# ORBITALS POSSIBLE
Consider the #2p# orbitals as a simpler example.
When you have #m_l = -1, 0, +1#, you know you get three orbitals: #2p_x#, #2p_y#, and #2p_z#, but #m_l# only correlates with three orbitals without further explanation.
You could also take the #2p_z# orbital and think of it another way. If you want the angular momentum in the #z# direction, you can examine the following angular part of the Schrodinger equation in spherical coordinates:
#hatL_zY_l^(m_l)(theta,phi) = m_lℏY_l^(m_l)(theta,phi)#
resembling #hatHpsi = Epsi#.
Without getting into too many complicated details (you don't have to know the three expressions for the #Y_(l)^(m_l)(theta,phi)#), you can assert that the #z# angular momentum #L_z# can be expressed for three different #m_l# values, which trace out the #2p_z# orbital in units of #ℏ#, where #ℏ = h/(2pi)# and #h# is Planck's constant.
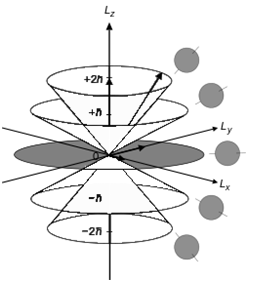
You have three relevant #m_l# projections depicted (ignore the #pm2ℏ#; that's because the diagram is of a #d# orbital, but we can apply it to the #2p_z# orbital):
- #m_l = -1 -> L_z => -ℏ# (forming the bottom lobe, labeled #-ℏ#)
- #m_l = 0 -> L_z => 0# (forming the central dot, or node, labeled #0#)
- #m_l = +1 -> L_z => ℏ# (forming the top lobe, labeled #ℏ#)
Naturally, the top lobe is symmetrically-shaped in relation to the bottom lobe.
THE ORTHOGONALITY CONDITION
Now, a quantum mechanical postulate/requirement for an orbital is that it be orthogonal (perpendicular) to all the other possible orbitals.
Two mathematical ways of conveying that are the dot product and the cross product:
#hatxcdothaty = <<1,0,0>> cdot <<0,1,0>> = 0#
#hatxcdothatz = <<1,0,0>> cdot <<0,0,1>> = 0#
#hatycdothatz = <<0,1,0>> cdot <<0,0,1>> = 0#
#hatx xxhaty = <<1,0,0>> xx <<0,1,0>> = <<0,0,1>> = hatz#
#haty xxhatz = <<0,1,0>> xx <<0,0,1>> = <<1,0,0>> = hatx#
#hatz xxhatx = <<0,0,1>> xx <<1,0,0>> = <<0,1,0>> = haty#
Since the #2p_z# lies along the #z# axis and since the #z# axis is the #2p_z# orbital's axis of symmetry, the only way the other orbitals can be orthogonal is that they lie along the #\mathbf(x)# and #mathbf(y)# axes (as you may have recognized in the pattern from the above dot and cross products).
Clearly, the #x#, #y#, and #z# axes, as you've seen many times in #xyz# coordinate systems, are perpendicular.
As a result of #m_l = -1, 0, +1# as well as the orthogonality condition, there are three orbitals possible: #2p_x#, #2p_y#, and #2p_z#.
Similarly, because there are #7# values of #m_l# for the #4f# orbitals, they are constructed to be particularly shaped according to the above angular momentum Schrodinger equation, in such a way that they are all orthogonal to each other.
There just happens to be #7# different orbital shapes that are all orthogonal to each other, just in more complex ways than the #2p# example.


