Question

Does the normalized radial probability density `4pir^2R_(nl)^2(r)` give the probability you have of finding an electron a certain distance `r` away from the nucleus?

Answer 1

It's a common mistake to say that this is true, when it strictly speaking, it is not.

If you consider how a Gaussian distribution works, you'd be on the right track.

The probability density is saying that if you integrate (i.e. find the area under the curve) from distance A to distance B away from the center of the orbital, there is a specific probability of finding an electron. In other words:

`color(blue)(int_a^b psi^"*"psid tau = "Probability")`

But the coordinate `(r,r^2R_(nl)^2(r))` does not say that you will have a `r^2R_(nl)^2(r)%` of finding an electron `r` distance away from the center of the orbital. The integral from `r_1` to `r_2` does.

The probability density is basically a time-dependent distribution plot as to which places the electron appears most often.

If referencing only the coordinates, all we know is where it shows up most often, not how often it shows up there.

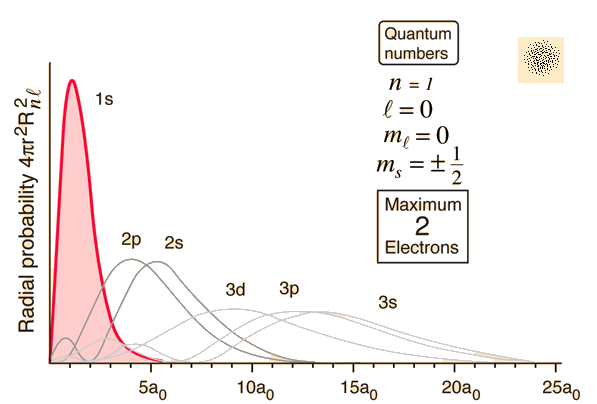
Here are some observations we CAN say, in reference to the center of each orbital:

• The probability of finding a `2s` electron at `2` bohr radii (`a_0 = 5.29177xx10^(-11)` `"m"`) is `0%`.
• The probability of finding a `1s` electron is highest at approximately `1` bohr radius.
• There is a `0%` chance you can find electrons at all if you look past about `24a_0`, even for the `3s` orbital.
• On average, the `2s` electron can be found most often at a farther distance away from the center of the orbital than a `2p` electron.

CHALLENGE: How many nodes are in a `2s` orbital? How about a `3p`?