How do you convert #x^2 - y^2 = 5# in polar form?
1 Answer
The polar form of that equation will be r=
Explanation:
To solve this problem, you have to understand the relationship that x and y has with r. r is the radius and has a starting point on the origin with an ending point anywhere on the graph. However, to use r in math, you have to break it into components since the angle provides challenges with calculations. The x component is how far away it is left or right from the origin. The y component is how far it is up or down from the origin. Together, the x and y components with r make a right triangle like so:
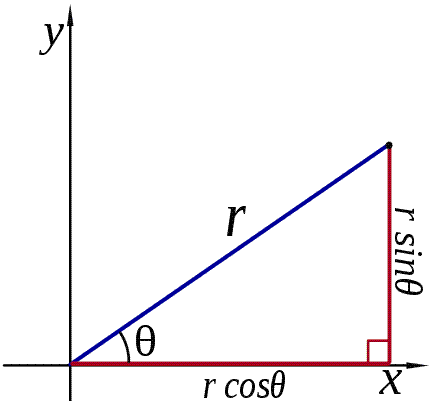
The x component is the adjacent side to the angle, so use cosine (Cosine
x= rcos
The y component is the opposite side to the angle, so use sine (Sine
y = rsin
Now that you know what x and y equals, plug them in to the equation.
Square both sides to get
Factor out the
Using the trigonometry identity of cos(2θ)=
(just have to memorize that identity)
Divide both sides by cos(2θ) to isolate r.
Square root it
r=
However since a square root can't be negative, there are some limits to the domain of cos(2θ).
Normally, cosθ is positive from -
However, since the angle is doubled in cos(2θ), divide by two.
This yields the final domain for this function to be -

