Question

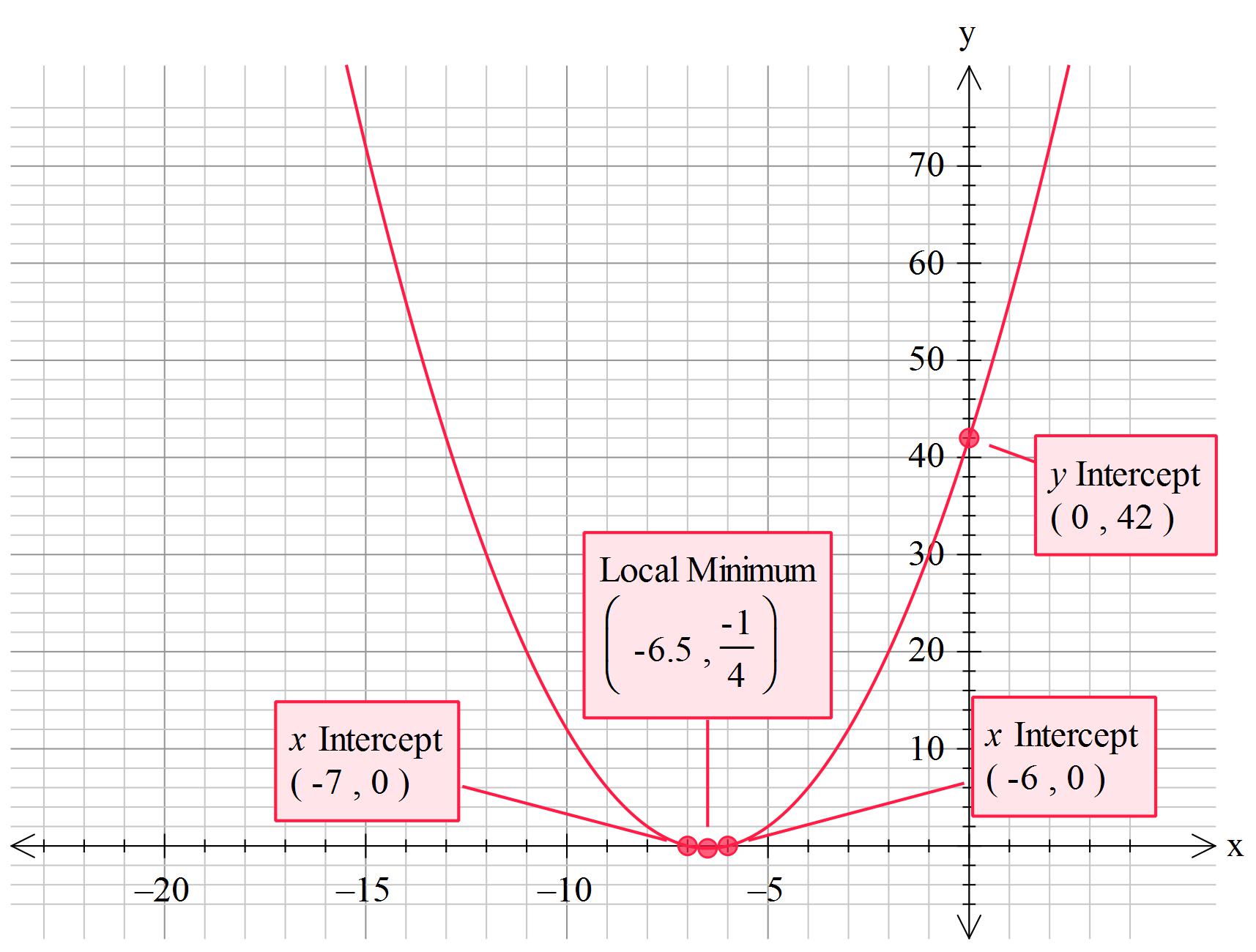
How do you solve using the completing the square method `x ^2 + 13 x + 42 = 0`?

Answer 1

For a very detailed example of method see
http://socratic.org/s/asVauX76

`"Vertex" ->(x,y)=(-13/2 -1/4) = (-6 1/2,-1/4)`
I will let you solve the other bits!

Explanation:

Given:`" "x^2+13x+42=0`

The process applied introduces an error that is removed by adding the correction factor of `k`

Write as:`" "(x^2+13x)+42=0`

Add the correction factor of `k`

`" "(x^2+13x)+42+k=0`

Take the power to outside the brackets

`" "(x+13x)^2+42+k=0`

Halve the coefficient of `13x`

`" "(x+13/2 x)^2+42+k=0`

Remove the `x` from `13/2 x`

`" "(x+13/2)^2+42+k=0`

The error comes from `(+13/2)^2 =+ 169/4`

So `k=-169/4` giving:

`" "(x+13/2)^2+42-169/4=0`

`" "(x+13/2)^2 -1/4=0`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`"Vertex" ->(x,y)=(-13/2 -1/4) = (-6 1/2,-1/4)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Find x-intercepts by substituting 0 for y and solve in the normal way
y-intercept is the constant in the original equation = +42

I will let you solve for the x-intercepts