Question

How do you find the asymptotes for `(x^3-8)/(x^2-5x+6)`?

Answer 1

Vertical asymptote is `x = 3`

No horizontal asymptote

Oblique asymptotes is `y=x+5`

Explanation:

First, we simplify the given function.

Factorize the numerator:

`x^3-8=x^3-2^3`

This is of the form `a^3-b^3`
And we know that `a^3-b^3=(a-b)(a^2 +ab+b^2)`

Therefore, `x^3-2^3 = (x-2)(x^2+2x+4)`

Factorize the denominator:

`x^2-5x+6`

The given equation is a quadratic equation, of the form:

`ax^2+bx+c=0`

Where, `a=1, b=-5, c=6`

This equation can be solved using the quadratic formula.

`x_(1,2) = (-b+-sqrt(b^2-4ac))/(2a)`

The step-by-step walk through to solving the quadratic equation is given here

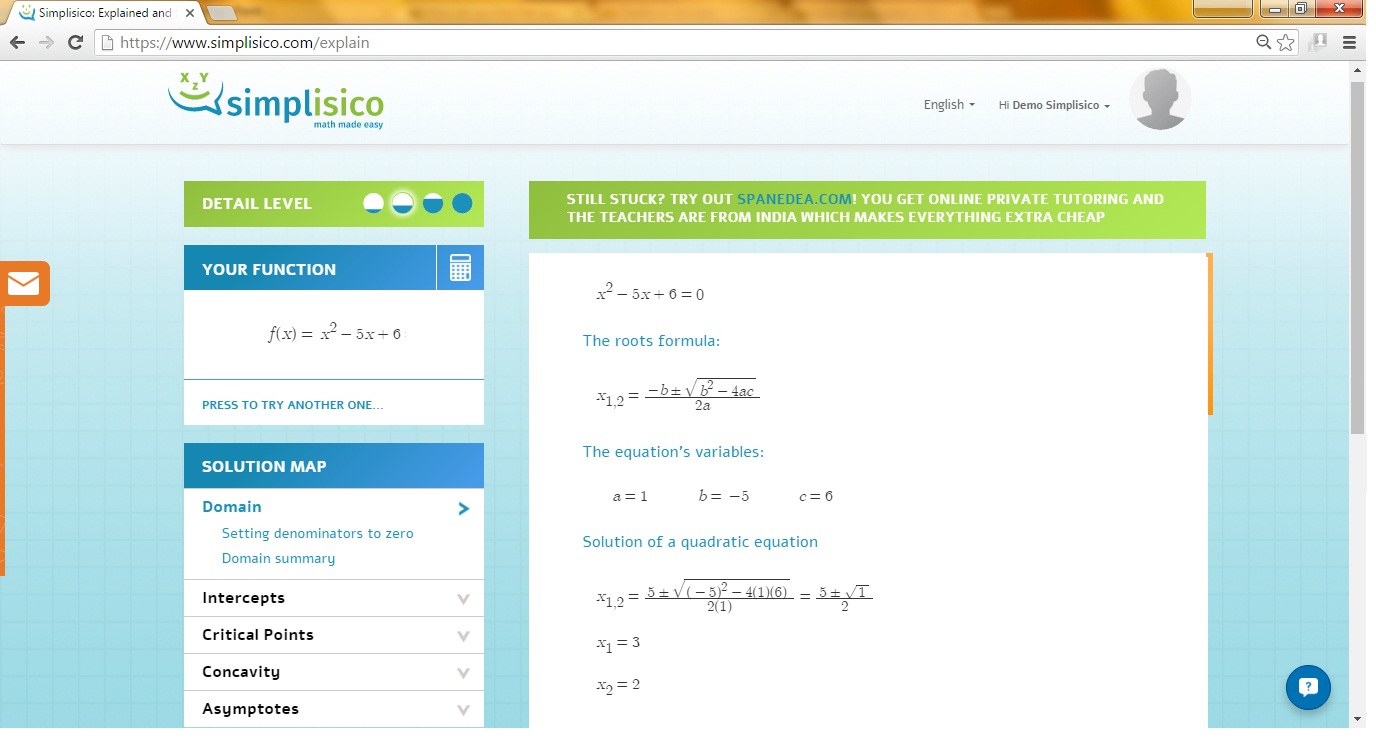
The factors are `(x-2)(x-3)`

Now rewriting the function as

`f(x)=((x-2)(x^2+2x+4))/((x-2)(x-3))`

Here, `(x-2)` is a common factor.

Our function is now `f(x)=(x^2+2x+4)/(x-3)`

Now we find the asymptotes.

An ASYMPTOTE is a line that approches a curve, but NEVER meets it.

To find the vertical asymptote , put the denominator = 0 (because 0 cannot divide any number) and solve.

Given below is the step-by-step walk through

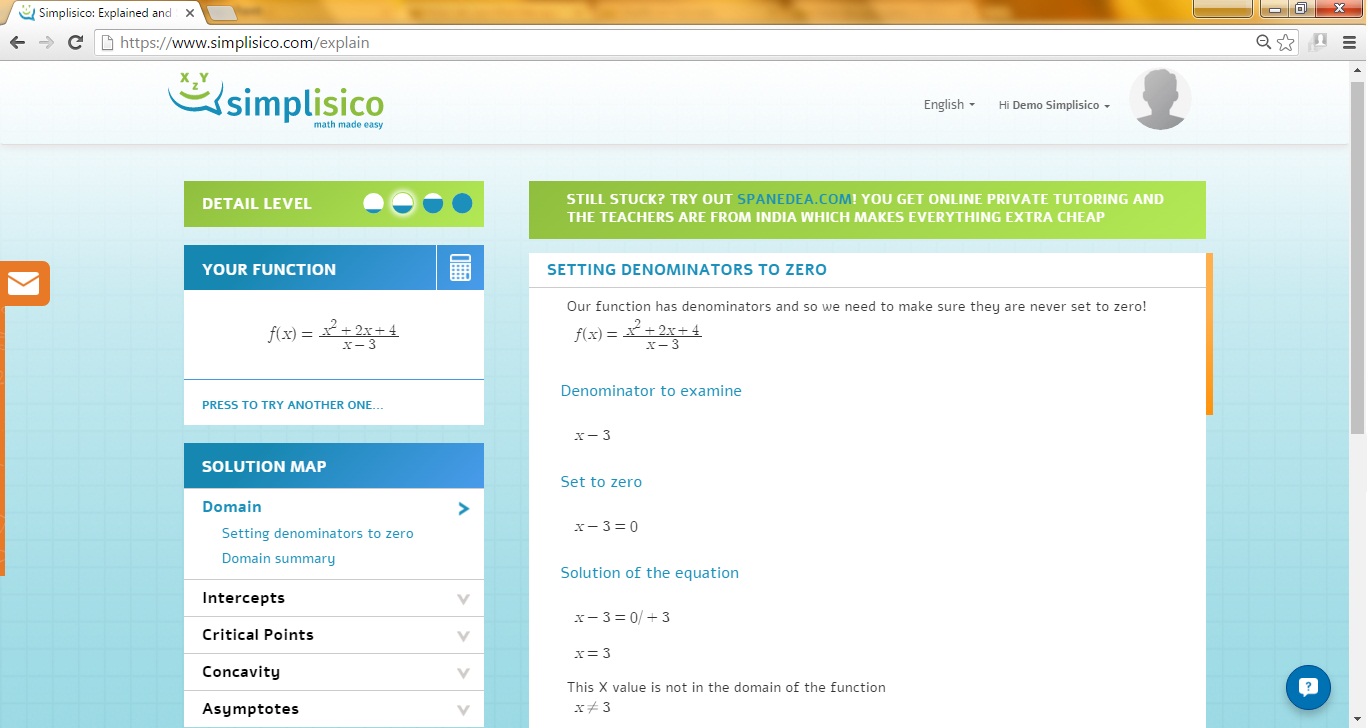
The curve will never touch the line `x=3`, thereby making it the vertical asymptote.

Next, we find the horizontal asymptote:
Compare the degree of the expressions in the numerator and the denominator.
Since the degree in the numerator is greater than the degree in the denominator, there are no horizontal asymptote.

The oblique asymptote is a line of the form y = mx + c.
Oblique asymtote exists when the degree of numerator = degree of denominator + 1

To find the oblique asymptote divide the numerator by the denominator.

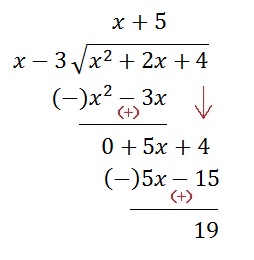
The quotient is the oblique asymptote.
Therefore, the oblique asymptote for the given function is `y=x+5`.