ABC is an acute angled triangle. The bisector of #/_# BAC intersects BC at D. BE is a perpendicular drawn on AC from B. Points E and D are joined. Show that #/_CED>45^o# How to show?
2 Answers
Some thoughts to begin an answer...
Explanation:
OK, here's a diagram to start:
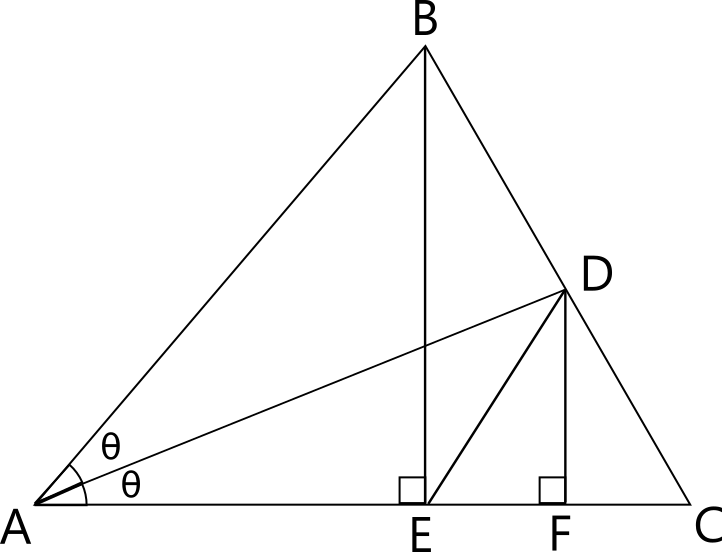
Let:
#{ (A = (0, 0)), (B = (e, h)), (C = (c, 0)), (D = (f, k)), (E = (e, 0)), (F = (f, 0)) :}#
Then:
#sin theta = (DF)/(AD) = k/sqrt(f^2+k^2)#
#cos theta = (AF)/(AD) = f/sqrt(f^2+k^2)#
#sin 2theta = (BE)/(AB) = h/sqrt(e^2+h^2)#
#cos 2theta = (AE)/(AB) = e/sqrt(e^2+h^2)#
From the double angle formulae we have:
#e/sqrt(e^2+h^2) = cos 2theta = cos^2theta - sin^2theta = (f^2-k^2)/(f^2+k^2)#
#h/sqrt(e^2+h^2) = sin 2theta = 2cos theta sin theta = (2fk)/(f^2+k^2)#
Since
#(f, k) = (c(1-t)+et, ht)#
We want to show that if
In other words,
Since the triangle is acute, there are some other conditions we can throw in:
#e > 0#
#e < c#
#AB^2+BC^2 > AC^2# , i.e.#sqrt(e^2+h^2)+sqrt((c-e)^2+h^2) > c^2#
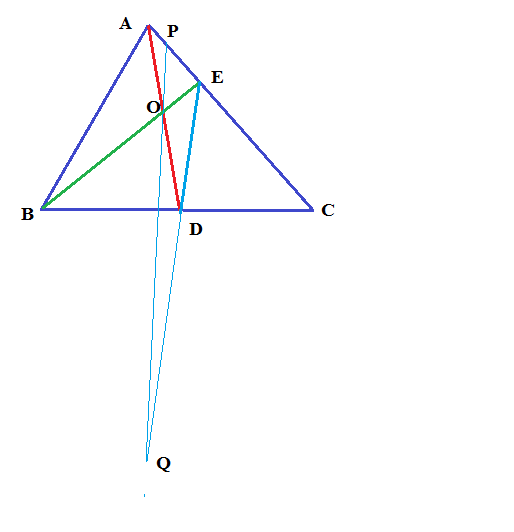
In acute angled
So
In
EP is taken equal in length of OE then P,O are joined and produced.
E,D are also joined and produced ,which meets the produced PO at Q.
Now in
So
Now in
the exterior
Hence


