Question

How do you find the vertical, horizontal or slant asymptotes for `f(x) = (x^2 - 2x + 1)/(x)`?

Answer 1

Vertical asymptote is `x = 0`

No horizontal asymptote

Oblique asymptotes is `y=x-2`

Explanation:

An ASYMPTOTE is a line that approches a curve, but NEVER meets it.

To find the vertical asymptote , put the denominator = 0 (because 0 cannot divide any number) and solve.

Here, `x=0`

The curve will never touch the line `x=0` or the `y`-axis, thereby making it the vertical asymptote.

Next, we find the horizontal asymptote:
Compare the degree of the expressions in the numerator and the denominator.
Since,
`color(red)("the degree in the numerator " >" the degree in the denominator")`
There are `color(red)("no horizontal asymptote")`.

The oblique asymptote is a line of the form y = mx + c.
Oblique asymtote exists when the degree of numerator = degree of denominator + 1

To find the oblique asymptote divide the numerator by the denominator.

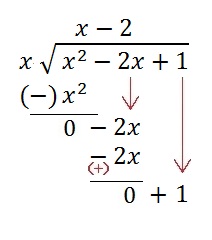
The quotient is the oblique asymptote.
Therefore, the oblique asymptote for the given function is `y=x-2`.