Question

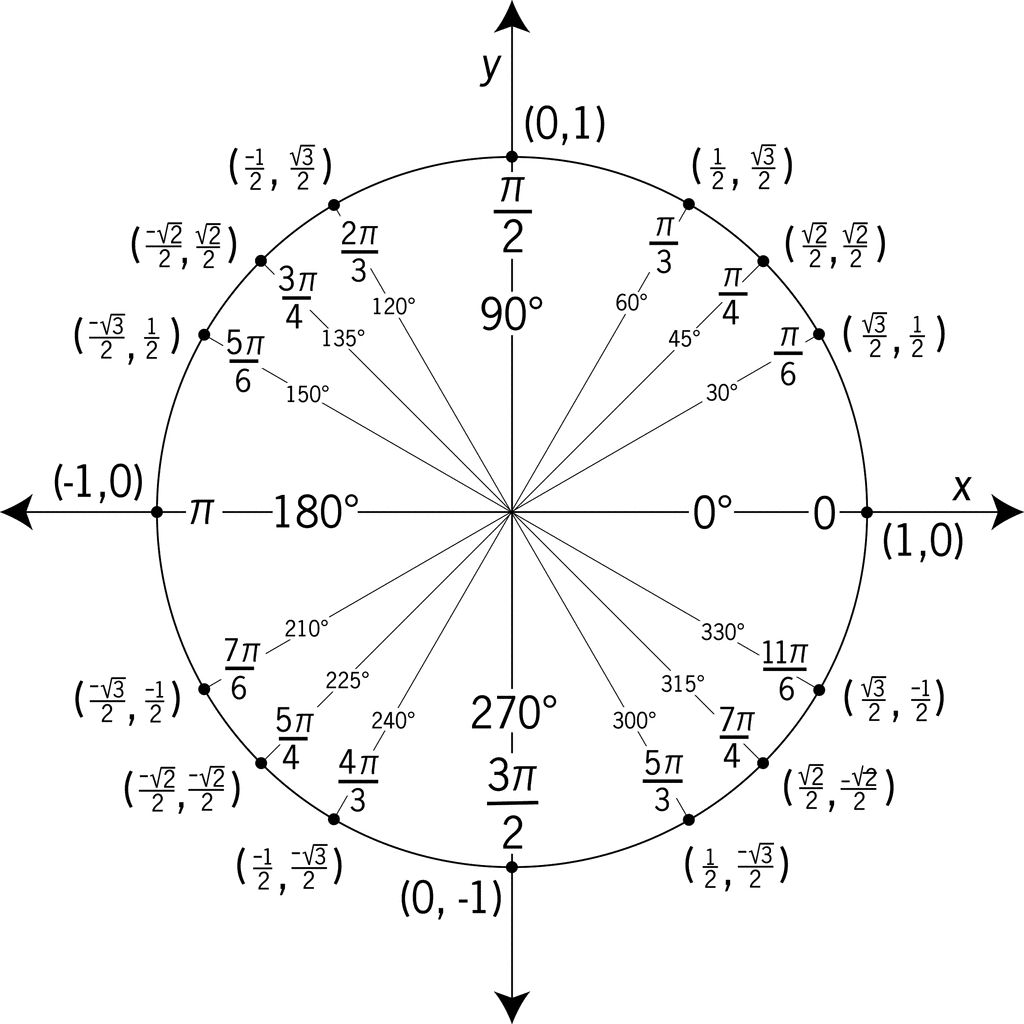
How do you find the exact value of `cos ((19pi)/6)`?

Answer 1

`-sqrt3/2`

Explanation:

Trig table, unit circle, and property of supplementary arcs -->
`cos ((19pi)/6) = cos (pi/6 + (18pi)/6) =`
`cos (pi/6 + 3pi) = cos (pi/6 + pi) = - cos pi/6 = - sqrt3/2`

Answer 2

`-sqrt3/2`

Explanation:

We can subtract `2pi` from `(19pi)/6` and still have the same value of cosine--the angles would be in the same location in the unit circle.

`(19pi)/6-2pi=(19pi)/6-(12pi)/6=(7pi)/6`

Thus, `cos((19pi)/6)=cos((7pi)/6)`.

Notice that `(7pi)/6=pi+pi/6`, so this angle is in `"QIII"` and has a reference angle of `pi/6`.

Since cosine is negative in `"QIII"`, and `cos(pi/6)=sqrt3/2`, we see that `cos((7pi)/6)=-sqrt3/2`.