Question

Question #20e24

Answer 1

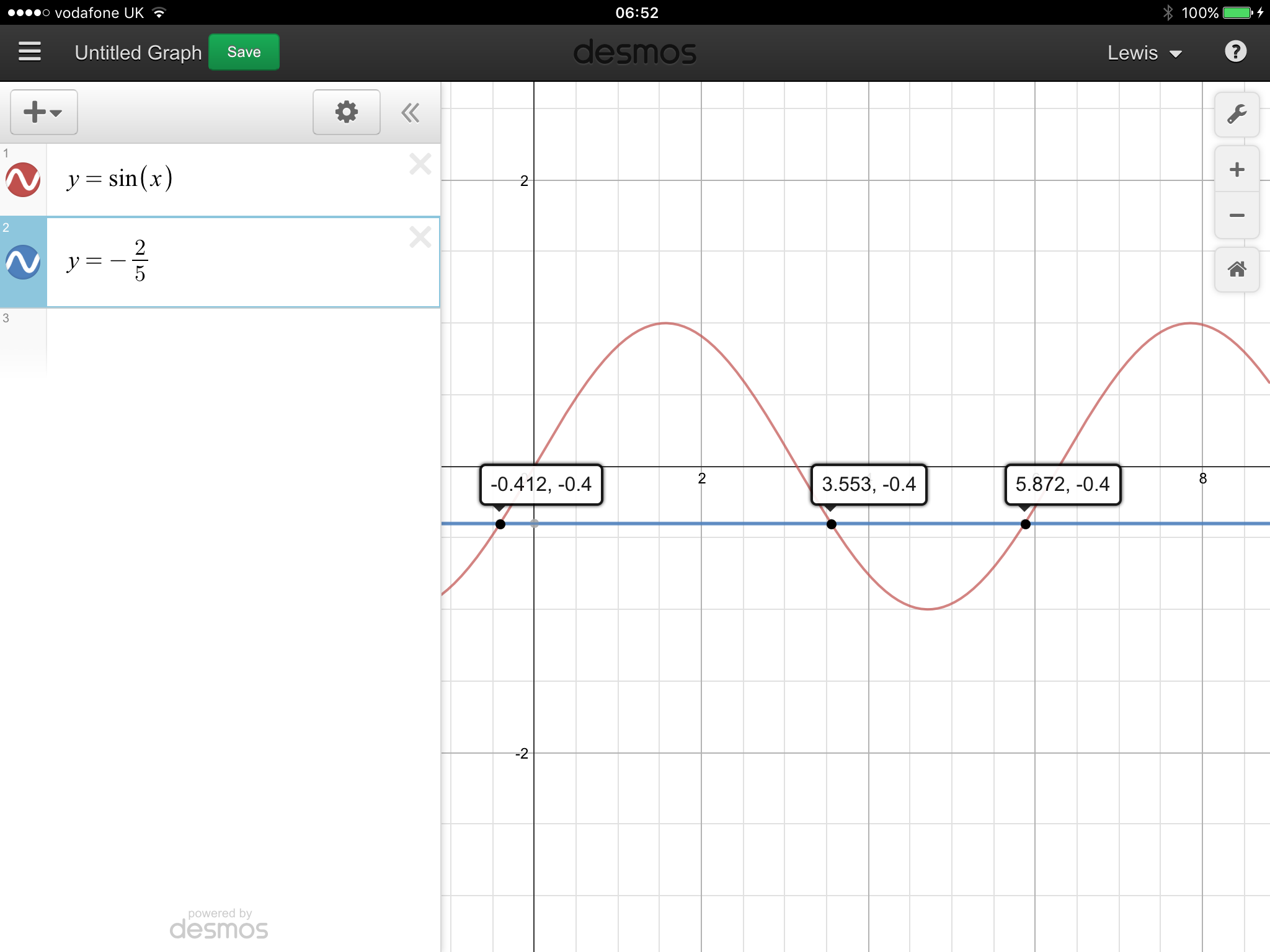
x = 3.553 and 5.872.

Explanation:

Firstly you use the arcsin function (`sin^-1`).
Starting with `sinx=-2/5`
If you take the inverse of sin to both sides:
`sin^-1(sinx)=sin^-1(-2/5)`
With inverse functions, they cancel out in this way. Like if you square the square root of x, you just get x.
Therefore, in this equation:
`x=sin^-1(-2/5)`
By putting this in your calculator (in radians, seeing as your domain is in radians) you will get `x=-0.412`.
This is called the principal value because it's just the first one your calculator selects, but you'll notice that it's not actually within your domain so it's not a solution.

As you can see in the image below, you can draw the line y=-2/5 on the graph of y=sinx in order to find where the solutions are. `x=3.553` and `x=5.872` are the only ones in the domain specified above.

Alternatively, you can draw the graph yourself and imagine where the points would be. Therefore with your principal value of -0.412, you can take the absolute value (this is because we want the 'distance' from zero in the x direction) and then add it to `pi`. This will give you `x=3.553` and to get the other one just do 0.412 subtracted from `2pi` (to get `x=5.872`).

The above method is hard, as it requires you to think hard about how you will get your solutions in terms of 'distances'. Always draw the graph since how you do the 'distance' calculations depends on where the solutions are and what graph is being used (sin/cos/tan, etc)