If #cos(theta) = (x-1)/(x+1)#, what is sin and tan of theta?
1 Answer
May 22, 2016
Explanation:
Here is a sketch to clarify.
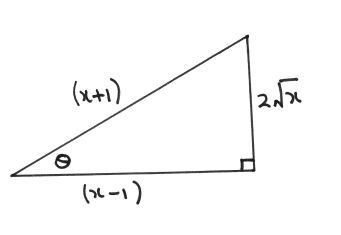
Given
We can identify the adjacent side (x-1) and the hypotenuse (x+1)
To find the opposite side (o) use
#color(blue)"Pythagoras' theorem"# For this right triangle then.
#(x+1)^2=(x-1)^2+o^2# expand using FOIL and collect like terms
#rArrx^2+2x+1=x^2-2x+1+o^2#
#rArro^2=cancel(x^2)-cancel(x^2)+2x+2xcancel(+1)cancel(-1)=4x# now
#o^2=4xrArro=sqrt(4x)=2sqrtx#
#rArrsintheta=(2sqrtx)/(x+1)" and " tantheta=(2sqrtx)/(x-1)#
