Question

How do you solve `sin^-1(x)+tan^-1(x)= pi/2`?

Answer 1

Despite that this form is comparable with the formula `sin^(-1)x+cos^(-1)x=pi/2`, it is not a formula. But the solution exists. See Truong-Son's answer

Explanation:

`sin(-1)0=npi and tan^(-1)0=mpi`, where m,n are 0, or any integer. So,

`sin(-1)0+tan^(-1)0= 0`, or an integer multiple of `pi`.

Despite that the form is comparable with the general formula `sin(-1)x+cos^(-1)x=pi/2`, there exists unique solution and this has been obtained by Truong-Son N.

Answer 2

I got `(sqrt(sqrt(5)/2 - 1/2),pi/2)` for the only solution to this equation.

---

First, let's see how many solutions this has by taking the derivative.

`d/(dx)[arcsinx + arctanx] = 0`

`= 1/(sqrt(1-x^2)) + 1/(1+x^2)`

Since neither term can be negative, we have no minimum or maximum, and thus, we have either one or zero solutions to this equation. This is also shown from the graph of `arcsinx + arctanx - pi/2 = 0` as follows:

graph{arcsinx + arctanx - pi/2 [-6.18, 7.87, -5.077, 1.95]}

Here's something interesting we can try...

`cos(arcsinx + arctanx) = cos(pi/2) = 0`

Now, recall the additive angle formula for `cos(upmv)`:

`cos(u + v) = cosucosv - sinusinv`

Since `arcsinx` and `arctanx` both yield an angle, we get:

`cos(arcsinx + arctanx)`

`= cos(arcsinx)cos(arctanx) - sin(arcsinx)sin(arctanx)`

`= color(red)(cos(arcsinx)cos(arctanx) - xsin(arctanx))`

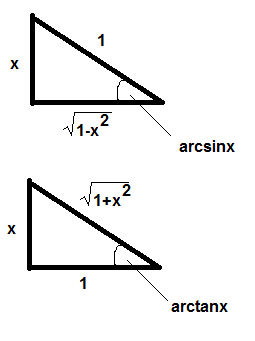
This should be handled with a triangle depiction now... Since `arcsin(x/1) = theta_1` and `arctan(x/1) = theta_2`, we have the following right-triangles:

Thus:

• `cos(arcsinx) = sqrt(1-x^2)`
• `cos(arctanx) = 1/sqrt(1+x^2)`
• `sin(arctanx) = x/(sqrt(1+x^2))`

Note that for each of these, since we started from positive `x` values for physically realistic triangle sides of length `x`, our solution for `arcsinx + arctanx = pi/2` must be positive to be valid. So, we proceed as follows:

`sqrt(1-x^2)/(sqrt(1+x^2)) - x^2/(sqrt(1+x^2)) = 0`

`(sqrt(1-x^2) - x^2)/(sqrt(1+x^2)) = 0`

`sqrt(1-x^2) - x^2 = 0`

`sqrt(1-x^2) = x^2`

`1-x^2 = x^4`

`x^4 + x^2 - 1 = 0 | x in [0,oo)`

Then, we can complete the square for this quartic equation to simplify it:

`x^4 + x^2 = 1`

`x^4 + x^2 + (1/2)^2 = 1 + (1/2)^2`

`x^4 + x^2 + 1/4 = 5/4`

`color(green)((x^2 + 1/2)^2 = 5/4 | x in [0,oo))`

Finally, solve for `x`. Remember that we can only take `x > 0`.

`x^2 + 1/2 = sqrt(5)/2`

`x^2 = sqrt(5)/2 - 1/2`

`color(blue)(x = sqrt(sqrt(5)/2 - 1/2) ~~ 0.786)`

Indeed, Wolfram Alpha gets the same thing.

And the graph of `arcsinx + arctanx - pi/2 = 0` shows: