Question

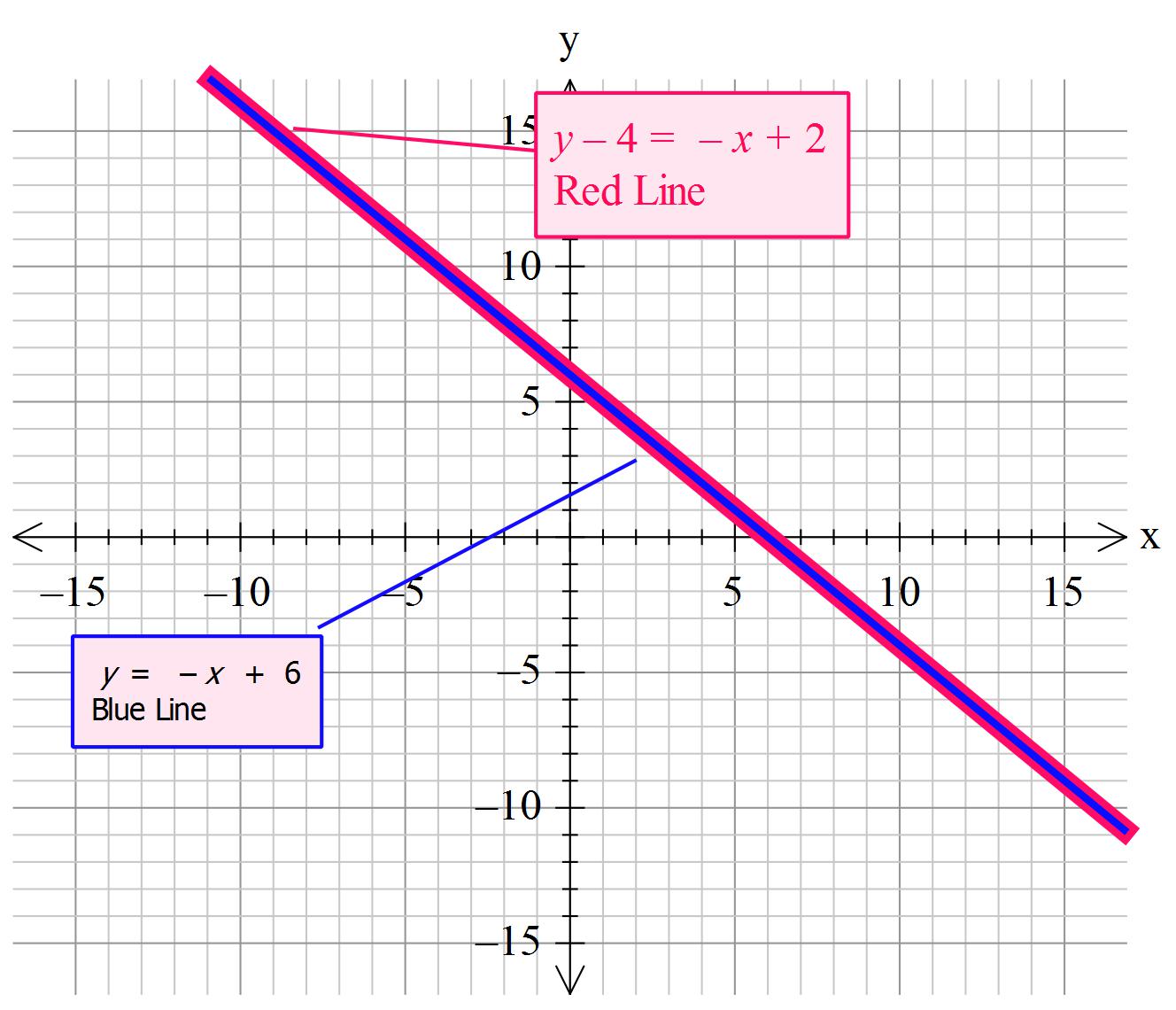
What is the equation of the line that passes through `(2,4)` and has a slope or `-1` in point-slope form?

Answer 1

`y-4=-(x-2)`

Explanation:

Given that gradient (m) `=-1`

Let some arbitrary point on the line be`(x_p,y_p)`

Known that gradient is `m=("change in y")/("change in x")`

We are given the point `(x_g,y_g)->(2,4)`

Thus

`m=("change in y")/("change in x") = (y_p-y_g)/(x_p-x_g) = (y_p-4)/(x_p-2)`

So we have `m=(y_p-4)/(x_p-2)`

Multiply both sides by `(x_p-2)`

`y_p-4=m(x_p-2) larr" This point-slope form"`

We are given that `m=-1`. So in general terms we now have

`y-4=-(x-2)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Note that although the value of `c` in `y=mx + c` is not stated in the point-slope form it is imbedded within the equation.

Let me show you what I mean: putting `m` back

`y-4=m(x-2)`

`y-4=mx-2m`

`y=mx-2m+4`

So `c=-2m+4`

So for this equation `c=-2(-1)+4 = +6`