A triangle has corners at points A, B, and C. Side AB has a length of #12 #. The distance between the intersection of point A's angle bisector with side BC and point B is #7 #. If side AC has a length of #21 #, what is the length of side BC?
1 Answer
May 25, 2016
BC=19.25
Explanation:
Here is a sketch (not to scale)
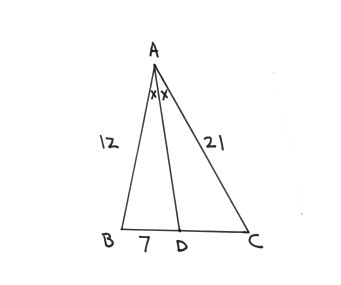
To calculate the length of BC ,we require to find the length of DC.
This can be done by using the
For triangle ABC this is.
#color(red)(|bar(ul(color(white)(a/a)color(black)((BD)/(DC)=(AB)/(AC))color(white)(a/a)|)))# Substitute the appropriate values into the ratio.
#rArr7/(DC)=12/21# now cross-multiply
#rArrDCxx12=7xx21rArrDC=(7xx21)/12=12.25# Thus BC = BD + DC = 7 + 12.25 = 19.25
