#color(blue)("Determine vertical asymptotes")#
Mathematically you are not allowed to divide by 0. This situation is called 'undefined'.
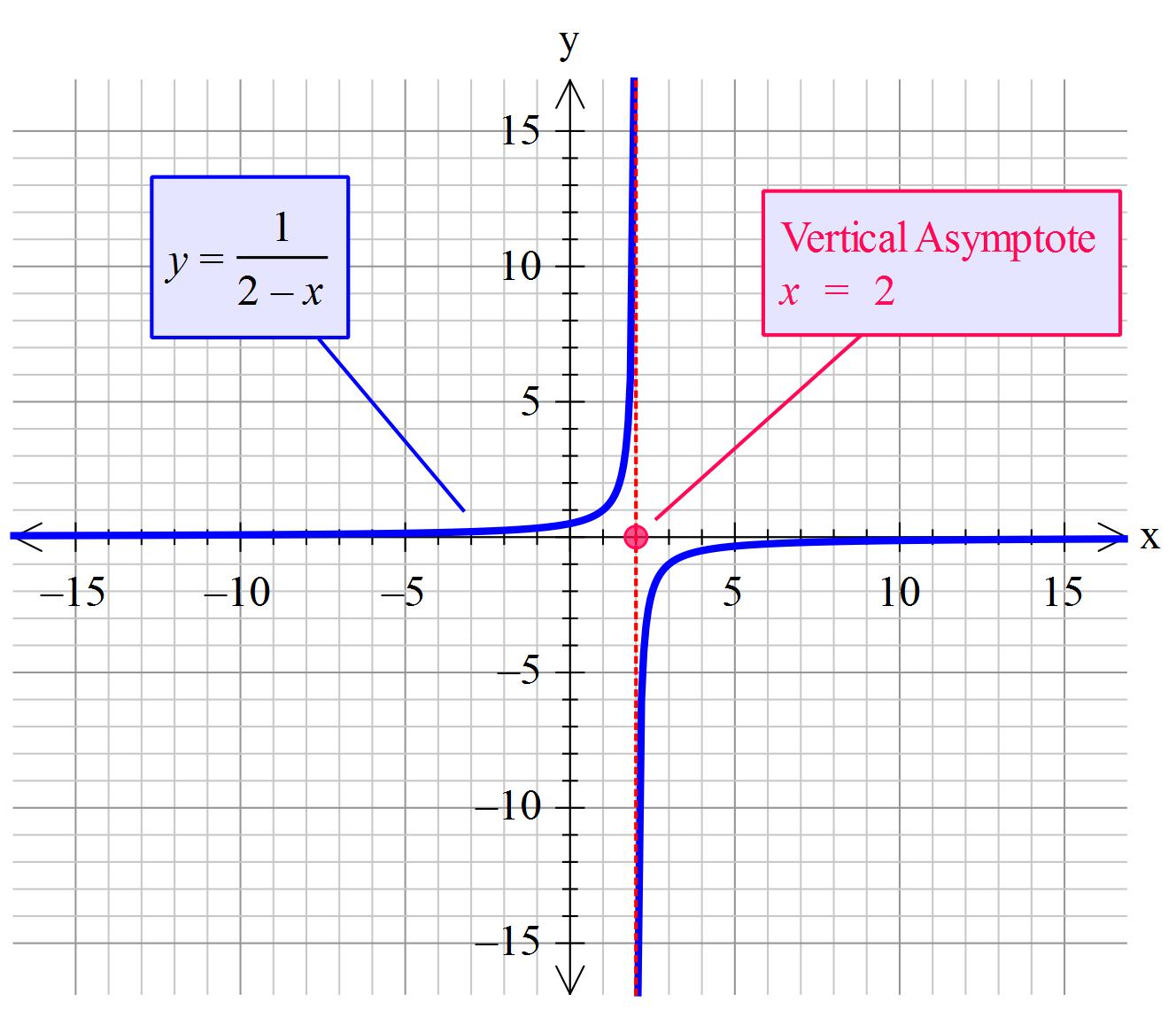
So at #x=2# the equation is undefined. Thus #x=2# is an asymptote.
Suppose #x>2# then #2-x < 0#
As #x# becomes increasingly closer to 2 then #2-x# becomes smaller and smaller but still negative.
In the same way, when #x<2# but approaching 2 then #2-x# becomes smaller and smaller but is still positive.
'
So #1/(2-x)# becomes increasingly larger but negative or positive depending on what side of 2 we find #x# to be.
'...................................................................
When writing limits; when approaching a value from the positive side then for the value 2 it would be written as #color(white)()^(+)2#
Same way for approaching from the negative side it is #color(white)()^(-)2#
Thus
# y = lim_(xtocolor(white)()^(+)2)1/(2-x) = - oo " "larr ( x > 2)#
# y = lim_(xtocolor(white)()^(-)2)1/(2-x) = + oo " "larr (x<2)#
#color(green)("So "x=2 " is the vertical asymptote")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)( "Determine horizontal asymptotes")#
# y = lim_(xtocolor(white)()^(+) oo)1/(2-x) = 1/(2-oo) =- 1/oo = color(white)()^(-) 0#
# y = lim_(xtocolor(white)()^(-) oo)1/(2-x) = 1/(2+oo) = +1/oo = color(white)()^(+) 0#
#color(green)("So "y=0 " is the horizontal asymptote")#
