Let #vec(x)# be a vector, such that #vec(x) = (−1, 1), " and let " R(θ) = [(costheta, -sintheta), (sintheta, costheta )]#, that is Rotation Operator. For #theta=3/4pi# find #vec(y) = R(theta)vec(x)#? Make a sketch showing x, y, and θ?
1 Answer
This turns out to be a counterclockwise rotation. Can you guess by how many degrees?
Let
#T(vecx) = R(theta)vecx,#
#R(theta) = [(costheta,-sintheta),(sintheta,costheta)],#
#vecx = << -1,1 >>.#
Note that this transformation was represented as the transformation matrix
What it means is since
#[(costheta,-sintheta),(sintheta,costheta)]xx<< -1,1 >>#
For an
#[(y_(11),y_(12), . . . , y_(1n)),(y_(21),y_(22), . . . , y_(2n)),(vdots,vdots, ddots , vdots),(y_(m1),y_(m2), . . . , y_(mn))]#
#= [(R_(11),R_(12), . . . , R_(1k)),(R_(21),R_(22), . . . , R_(2k)),(vdots,vdots, ddots , vdots),(R_(m1),R_(m2), . . . ,R_(mk))]xx[(x_(11),x_(12), . . . , x_(1n)),(x_(21),x_(22), . . . , x_(2n)),(vdots,vdots, ddots , vdots),(x_(k1),x_(k2), . . . , x_(kn))]#
Therefore, for a
Multiplying these two gives:
#[(costheta,-sintheta),(sintheta,costheta)]xx[(-1),(1)]#
#= [(-costheta - sintheta),(-sintheta + costheta)]#
Next, we can plug in
#color(blue)(T(vecx) = R(theta)vecx)#
#= R(theta)[(-1),(1)]#
#= [(-cos((3pi)/4) - sin((3pi)/4)),(-sin((3pi)/4) + cos((3pi)/4))]#
#= [(-cos135^@ - sin135^@),(-sin135^@ + cos135^@)]#
#= [(-(-sqrt2/2) - sqrt2/2),(-sqrt2/2 + (-sqrt2/2))]#
#= color(blue)([(0),(-sqrt2)])#
Now, let's graph this to see what this looks like. I can tell that it's a counterclockwise rotation, after determining the transformed vector.
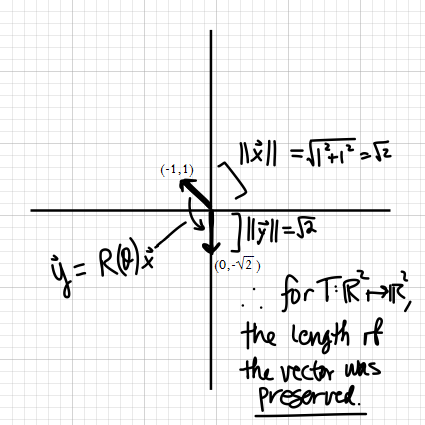
Indeed, a counterclockwise rotation by
CHALLENGE: Maybe you can consider what happens when the matrix is

