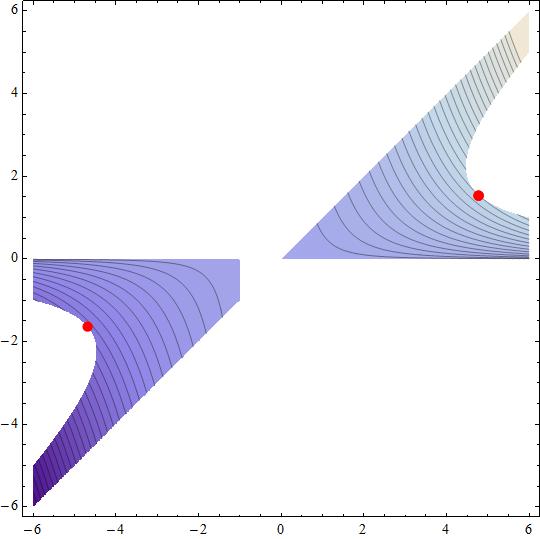
We will searching for stationary points, qualifying then as local maxima/minima.
First we will transform the maxima/minima with inequality restrictions into an equivalent maxima/minima problem but now with equality restrictions.
To do that we will introduce the so called slack variables #s_1# and #s_2# such that the problem will read.
Maximize/minimize #f(x,y) = x sqrt[x y + y]#
constrained to
#{
(g_1(x,y,s_1)=x y - y^2 - s^2=0),
(g_2(x,y,s_2)=x y - y^2 + s_2^2 - 5=0)
:}#
The lagrangian is given by
#L(x,y,s_1,s_2,lambda_1,lambda_2) = f(x,y)+lambda_1 g_1(x,y,s_1)+lambda_2g_2(x,y,s_2)#
The condition for stationary points is
#grad L(x,y,s_1,s_2,lambda_1,lambda_2)=vec 0#
so we get the conditions
#{
(lambda_1 y + lambda_2 y + (x y)/(2 sqrt[y + x y]) + sqrt[y + x y] = 0),
(lambda_1 (x - 2 y) + lambda_2 (x - 2 y) + (x (1 + x))/(2 sqrt[y + x y]) = 0),
( -s_1^2 + x y - y^2 = 0),
(-2 lambda_1 s_1 = 0),
(-5 + s_2^2 + x y - y^2 = 0),
(2 lambda_2 s_2 = 0)
:}#
Solving for #{x,y,s_1,s_2,lambda_1,lambda_2}# we have
#{(x = -4.69709, y = -1.63044, lambda_1 = 0., s_1 = -2.23607,lambda_2 = 2.4624,s_2 = 0.),
(x = 4.78125, y = 1.54499, lambda_1 = 0., s_1 = -2.23607,
lambda_2 = -2.73431, s_2 = 0.)
:}#
so we have two points
#p_1={-4.69709, -1.63044}#
and
#p_2 = { 4.78125, 1.54499}#
Point #p_1# activates restriction #g_2(x,y,0)=0,{lambda_2 ne 0, s_2 = 0}#
Point #p_2# activates restriction #g_2(x,y,0)=0,{lambda_2 ne 0, s_2 = 0}#
#p_1# is qualified with #f_{g_2}(x)=(x sqrt[(1 + x) (x + sqrt[ x^2-20])])/sqrt[2]#
and
#p_2# is qualified with #f_{g_2}(x)#
Computing
#d/(dx)(f_{g_2}(-4.69709)) = 0#
and
#d^2/(dx^2)(f_{g_2}(-4.69709)) = -8.19783#
we conclude that #p_1# local maximum point.
Analogously for #p_2#
#d/(dx)(f_{g_2}(0)) = 4.78125#
and
#d^2/(dx^2)(f_{g_2}( 4.78125)) = 6.22258#
so #p_1,p_2# are local maximum and minimum points