How do you find the exact relative maximum and minimum of the polynomial function of #f(x) = x^3 - 6x^2 + 9x +1#?

Question

2188 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-10T15:05:59

#(1, 5)# Maximum Point
#(3, 1)# Minimum Point

Given #f(x)=x^3-6x^2+9x+1#

Find the first derivative #f' (x)# then equate to zero then solve for the point.

#f(x)=x^3-6x^2+9x+1#

#f' (x)=3x^2-12x+9#

#f' (x)=3x^2-12x+9=0#

#x^2-4x+3=0#

#(x-1)(x-3)=0#

#x-1=0# and #x-3=0#

#x=1# and #x=3#

At #x=1#

#f(x)=x^3-6x^2+9x+1#

#f(1)=1^3-6(1)^2+9(1)+1#

#f(1)=1-6+9+1#

#f(1)=5#

At #x=3#

#f(x)=x^3-6x^2+9x+1#

#f(1)=(3)^3-6(3)^2+9(3)+1#

#f(1)=27-54+27+1#

#f(1)=1#

So the points are #(1, 5)# and #(3, 1)#

#(1, 5)# Maximum Point
#(3, 1)# Minimum Point

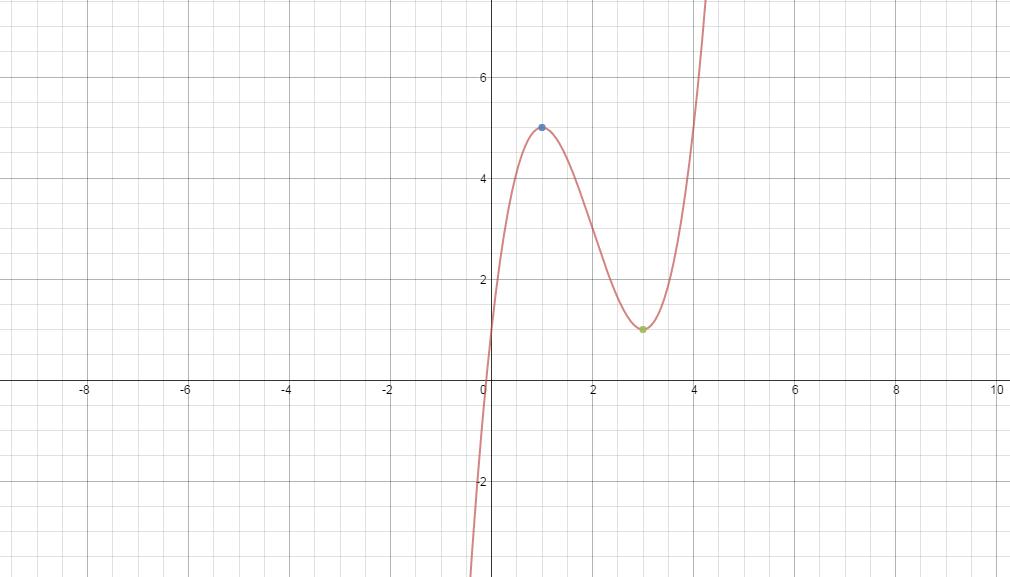
Desmos

God bless....I hope the explanation is useful.