Introducing the so called slack variables s_1, s_2s1,s2 the optimization problem is transformed into an equivalent one
Find local minima, maxima of
f(x,y)= x^2+y^3f(x,y)=x2+y3
subject to
g_1(x,y,s_1) = x + 3 x y - s_1^2 = 0g1(x,y,s1)=x+3xy−s21=0
g_2(x.y,s_2)=x+3 x y + s_2^2-4=0g2(x.y,s2)=x+3xy+s22−4=0
The lagrangian is
L(x,y,s_1,s_2,lambda_1,lambda_2) = f(x,y)+lambda_1 g_1(x,y,s_1)+lambda_2g_2(x,y,s_2)L(x,y,s1,s2,λ1,λ2)=f(x,y)+λ1g1(x,y,s1)+λ2g2(x,y,s2)
LL is analytical so the stationary points include the relative maxima and minima.
The determination of stationary points is done solving for x,y,s_1,lambda_1,s_2,lambda_2x,y,s1,λ1,s2,λ2 the system of equations given by
grad L(x,y,s_1,lambda_1,s_2,lambda_2) = vec 0∇L(x,y,s1,λ1,s2,λ2)=→0
or
{(2 x + lambda_1 (1 + 3 y) + lambda_2 (1 + 3 y)=0),
(3 lambda_1 x + 3 lambda_2 x + 3 y^2=0),
( -s_1^2 + x + 3 x y=0),
(-2 lambda_1 s_1=0),
(-4 + s_2^2 + x + 3 x y=0)
,( 2 lambda_2 s_2=0)
:}
Solving we get
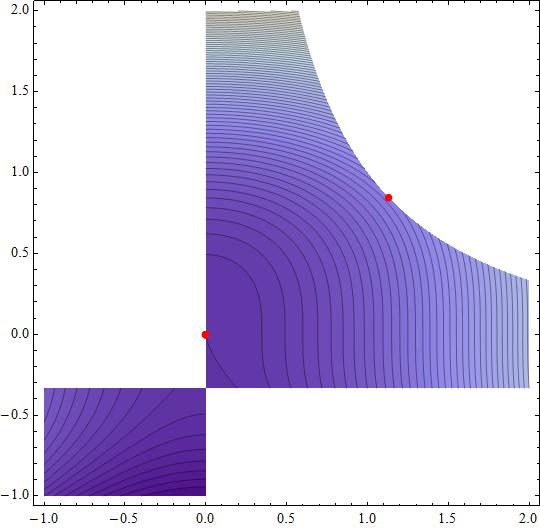
(x=0., y = 0., lambda_1 = 0., s_1 = 0., lambda_2= 0., s_2= 2.)
and
(x= 1.12872, y= 0.847942, lambda_1=0., s_1 = 2., lambda_2 = -0.637008, s_2 = 0.)
Both points are at the boundaries of g_1(x,y,0)=0 and g_2(x,y,0)=0 respectively.
Their qualification must be done with f_(g_1) and f_{g_2} respectively. So,
f_{g_1}(x) = x^2-1/27
f_{g_2}(x) = -(x-4)^3/(27 x^3) + x^2
d^2/(dx^2)f_{g_1}(0)=2 qualifying this point as a local minimum
d^2/(dx^2)f_{g_2}(1.12872) =11.5726 qualifying this point as a local minimum also
Attached a figure with a contour mapping with the found points