The tetrahedron enclosed by the coordinates planes and the plane 2x+y+z=4, how do you find the volume?
1 Answer
You don't even have to use integrals to find the volume, but you can, I guess.
I got
VISUAL APPROACH
For this plane, since it intersects with the
- Find the intersections
- Determine the length of each diagonal distance
- Find the volume of the entire hypothetical rhomboid pyramid
- Divide by
#4#
The intersections are at the
- One intersection is on the
#x# -axis, which is when#y = z = 0# . Thus,#x = 2# . - One intersection is on the
#y# -axis, which is when#x = z = 0# . Thus,#y = 4# . - One intersection is on the
#z# -axis, which is when#x = y = 0# . Thus,#z = 4# .
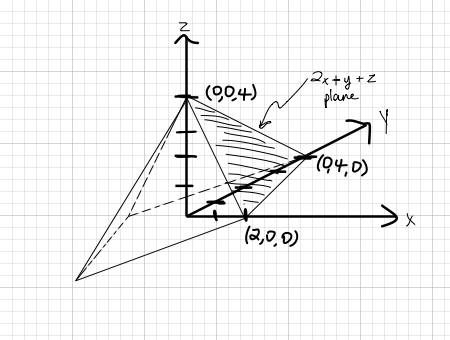
So, the three intersections are
- From the
#z# intersection, we get the height of the hypothetical rhomboid pyramid. - From the
#x# and#y# intersections, we get half of each diagonal distance across the hypothetical base.
The volume of the entire rhomboid pyramid would have been:
#\mathbf(V_"tetrahedron" = 1/3A_"base"h)#
The area of the symmetrical rhombus base is then four times the area of each triangular portion, which is the area enclosed by
#A_"base" = 4(1/2xy) = 2xy = 2(2)(4) = 16#
Or, we could have used the formula for the area of a rhombus ("diagonals method"), which uses
#A_"base" = (pq)/2 = ((2x)(2y))/2 = 2xy = 16#
Finally, by construction, the volume of the original tetrahedron is then one-fourth the volume of our hypothetical rhomboid pyramid:
#color(blue)(V_"tetrahedron") = 1/4[1/3Ah]#
#= 1/4*1/3[16*4]#
#= 1/4*64/3#
#= color(blue)(16/3)#
CALCULUS III APPROACH
An alternative approach to this using triple integrals involves integrating each dimension at a time.
#=> \mathbf(int_(x_1)^(x_2) int_(y_1)^(y_2) int_(z_1)^(z_2) dzdydx)#
What we have is
Next, to get the upper bounds, we solve the equation for each individual variable.
- Solving for
#z_2# , we get#color(green)(z_2 = 4 - 2x - y)# .
Note: our integration element can't have
#x = y = 0# , because#z = 4 - 2x# is our#xz# -plane triangle, and#y# allows us to integrate with respect to#y# later. This is our projection along the#\mathbf(y)# axis.
- Solving for
#y_2# , we note that in three dimensions, there exist two intersections on the#xy# -plane: when#x = 0# , and when#y = 0# . We can include both of them in one 2-variable equation when#z = 0# to get:
#color(green)(y_2 = 4 - 2x)# Note: our integration element can't have
#x = 0# , because#y = 4# is just a horizontal line, and we need to integrate with respect to#x# later. This is our projection along the#\mathbf(x)# axis.
- Solving for
#x_2# , we find where#4 - 2x# intersects the#x# -axis: when#z = 0# and#y = 0# . Therefore, we work from the initial equation to get:
#2x_2 = 4 - z - y => 2x_2 = 4#
#color(green)(x_2 = 2)#
Overall, we should picture the
- From above by the
#z = 4 - 2x - y# plane - From the upper-right of the
#xy# -plane by the#y = 4 - 2x# line - From the left by the
#yz# -plane - From the bottom by the
#xy# -plane
like so:
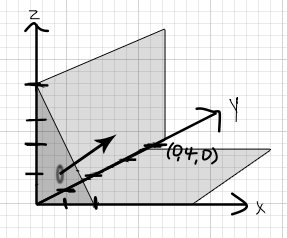
to generate the tetrahedron:
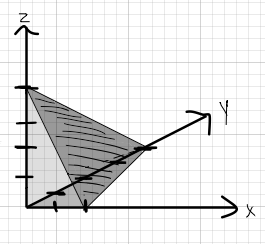
So, our integrals work out like this, from the inside out:
#int_(0)^(2) int_(0)^(4 - 2x) int_(0)^(4 - 2x - y) 1dzdydx#
#= int_(0)^(2) int_(0)^(4 - 2x) 4 - 2x - y dydx#
Now for the "partial" integral with respect to
#= int_(0)^(2) |[4y - 2xy - y^2/2]|_(0)^(4-2x) dx#
#= int_(0)^(2) [(4(4-2x) - 2x(4-2x) - (4-2x)^2/2) - cancel((4(0) - 2x(0) - (0)^2/2))] dx#
#= int_(0)^(2) [(16-8x) - (8x-4x^2) - (16 - 16x + 4x^2)/2] dx#
#= int_(0)^(2) [(16-8x) - (8x-4x^2) - (8 - 8x + 2x^2)] dx#
#= int_(0)^(2) 16 - 8x - 8x + 4x^2 - 8 + 8x - 2x^2 dx#
Finally, the integral with respect to
#= int_(0)^(2) 16 + 2x^2 - 8x - 8dx#
#= |[16x + 2/3x^3 - 4x^2 - 8x]|_(0)^(2)#
#= [16(2) + 2/3(2)^3 - 4(2)^2 - 8(2)] - cancel([16(0) + 2/3(0)^3 - 4(0)^2 - 8(0)])#
#= 32 + 16/3 - 16 - 16#
#= color(blue)(16/3)#
...which matches the more intuitive, visual approach! :)

