Question

How do you use the rational roots theorem to find all possible zeros of `f(x) = 3X^5 - 2X^2 + 16X - 2`?

Answer 1

Use a numerical method to find:

`x ~~ 0.12701`

`x ~~ 1.03966+-0.998855i`

`x ~~ -1.10317+-1.14378i`

Explanation:

`f(x) = 3x^5-2x^2+16x-2`

By the rational roots theorem, any rational zeros of `f(x)` are expressible in the form `p/q` for integers `p, q` with `p` a divisor of the constant term `-2` and `q` a divisor of the coefficient `3` of the leading term.

That means that the only possible rational zeros of `f(x)` are:

`+-1/3`, `+-2/3`, `+-1`, `+-2`

You can substitute each of these into the formula for `f(x)` to find that none of them is a zero.

So this quintic has no rational zeros.

`color(white)()`
By the fundamental theorem of algebra it does have exactly `5` Complex, possibly Real, zeros, counting multiplicity.

In addition, since its coefficients are Real, any non-Real Complex zeros must occur in Complex conjugate pairs.

Typically for a quintic, the zeros of this particular one are not expressible in terms of `n`th roots.

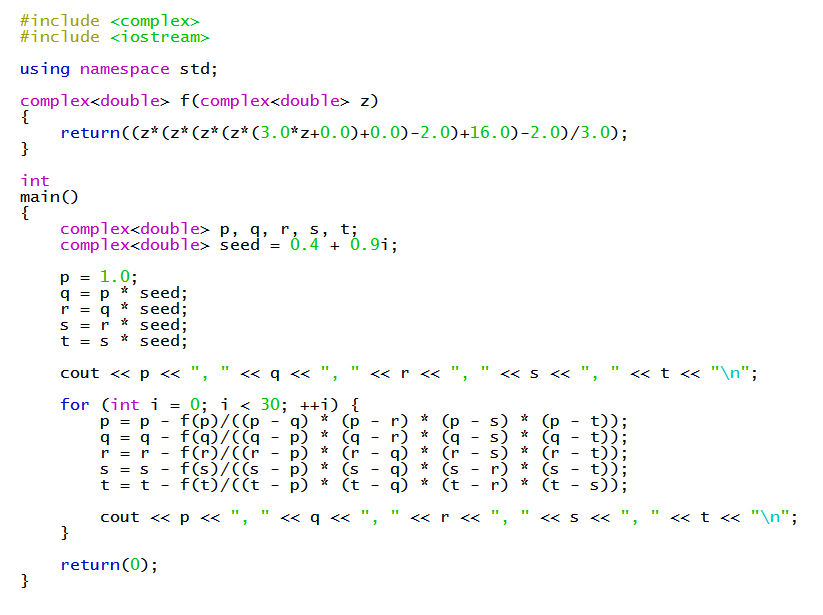
About the best we can do is find numeric approximations using a method like Durand-Kerner. See https://socratic.org/s/avyDEG5X for a fuller explanation, but the Durand-Kerner algorithm finds approximations for all `5` zeros at once.

The results I found were:

`x ~~ 0.12701`

`x ~~ 1.03966+-0.998855i`

`x ~~ -1.10317+-1.14378i`

Here's the C++ program I used to find them: