How do you use the triple integral to find the volume of the solid bounded by the surface #z=sqrt y# and the planes x+y=1, x=0, z=0?

Question

28584 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-27T11:41:00

#4/15#

first and key, because of the shape of #z = sqrt y# the plane y=0 is a boundary, in addition to the given x = 0, z = 0.

so we are in the first octant for all of this.

the further constraint is the plane x + y = 1

this is the best drawing i can muster

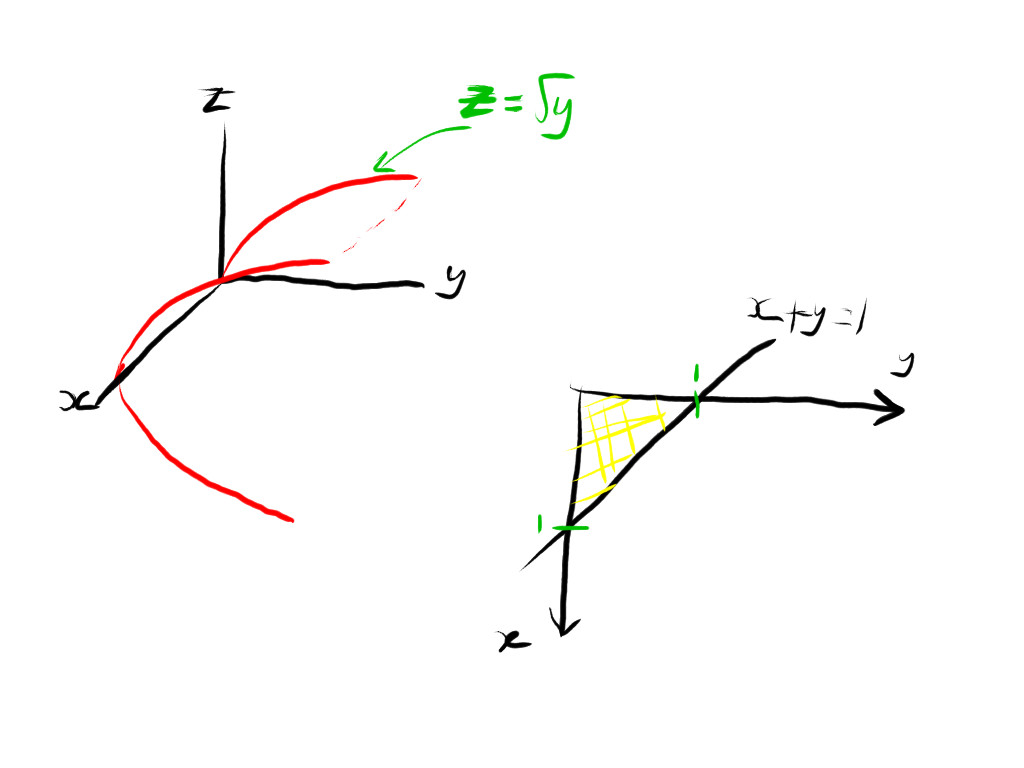
enter image source here

the yellow bit is the area over which we are integrating z(x,y)

but as a triple integral you would write:

#int_{x=0}^{1} \ int_{y=0}^{1-x} \ int_{z = 0}^{sqrt(y)} \ dz \ dy \ dx#

#= int_{x=0}^{1} \ int_{y=0}^{1-x} [z]_{z = 0}^{sqrt(y)} \ dy \ dx#

#= int_{x=0}^{1} \ int_{y=0}^{1-x} sqrt(y) \ dy \ dx#

#= int_{x=0}^{1} \ [2/3 y^{3/2}]_{y=0}^{1-x} \ dy \ dx#

#= int_{x=0}^{1} \ 2/3 (1-x)^{3/2} \ dx#

#= \ [- 4/15 (1-x)^{5/2} ]_{x=0}^{1}#

# = 4/15#

Answer 2 · 2016-06-27T13:20:15

4/15 cubic units

The surface of this solid comprises three planar sides (horizontal) z =

0 and (vertical) x = 0 and x + y +1 and a part, in the first octant, of the

(parabolic cross-sectional) cylinder z = #sqrt y#. This cylinder is

symmetrical about the xy-plane.

as z = #sqrt y, y>=0#..Being bounded below by z = 0, z does not

take negative #sqrt y# values.

Now, the volume of this solid in the first octant is

#V=int int int dz dy dx#, for z from 0 to #sqrt y#, y from o to 1-x and x

from 0 to 1.

Integrating with respect to z first, in order,,

#V=int inty^(1/2)dy dx#, y from 0 to 1-x and x from 0 to 1#

#=(2/3)int(1-x)^(3/2)dx#, x from 0 to 1

#=(2/3)(-2/5)(0-1)#

#=4/15# cubic units.