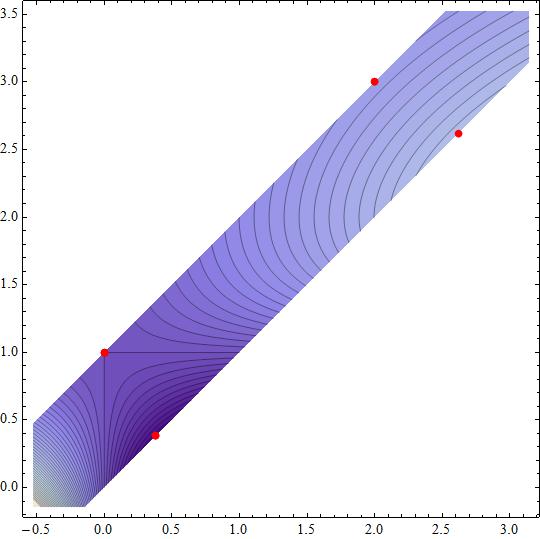
How do you minimize and maximize f(x,y)=(x^2+4y)/e^(y) constrained to 0<x-y<1?
1 Answer
There are local minima and local maxima points.
Explanation:
This problem will be solved using the Lagrange Multipliers technique.
(see https://en.wikipedia.org/wiki/Lagrange_multiplier)
This technique applies to analytic maximization/minimization problems with equality restrictions.
We will transform our problem which is with inequality restrictions into an equivalent one, now with equality restrictions. For this purpose we will introduce the so called slack variables
Minimize/Maximize
subjected to
The set of lagrangian stationary points contains the local minima/maxima points.
The lagrangian is stated as
The lagrangian stationary points are the solutions of
or
This nonlinear system of equations can be solved using a technique similar to Newton-Raphson's
(see https://en.wikipedia.org/wiki/Newton%27s_method)
obtaining
The first and the third are qualified by the restriction
The second and fourth are qualified by the restriction
The qualification is done over
So first and second points are local minima
the third and fourth points are local maxima.
Attached the