Question

A fence 4 feet tall runs parallel to a tall building at a distance of 2 feet from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building?

Answer 1

8.32ft

Explanation:

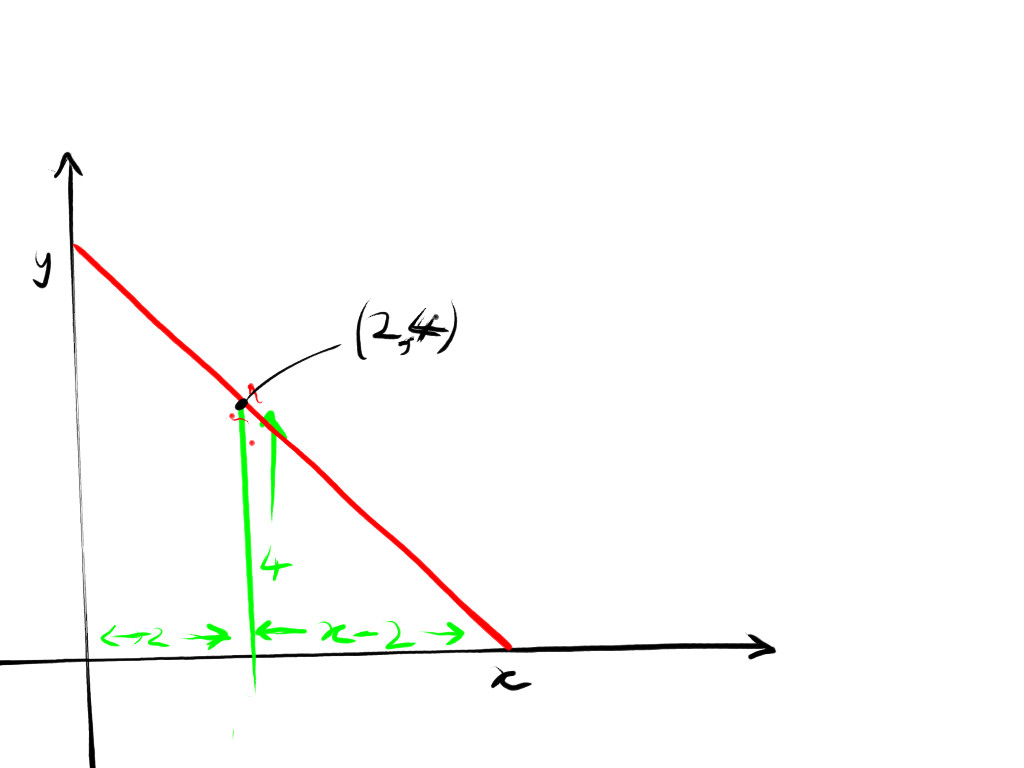
Intending to use a Lagrange Multiplier , we are minimising `s^2 = x^2 + y^2 = f(x,y)` where s is the length of the ladder.

This is subject to constraint which comes from similar triangles that `y/x = 4 / (x-2) \implies yx - 2y - 4x = 0 = g(x,y)`

so `nabla f = lambda nabla g = implies`

`<2x, 2y > = lambda < y - 4, x-2>`

`\implies x/(y-4) = y / (x-2) qquad star`

using the constraint `y/x = 4 / (x-2) \implies y = (4x)/(x-2)` and subbing this into `star` :

`\implies x/( (4x)/(x-2)-4) = ((4x)/(x-2)) / (x-2)`

`\implies (x(x-2))/( 4x-4(x-2)) = (4x) / (x-2)^2`

`\implies x(x-2)^3 = 32x`

`\implies x((x-2)^3 - 32) = 0`

ignoring the trivial solution we have

`(x-2)^3 = 32`

`x = 2 + 32^{1/3} = 5.175`

`y = 6.519`

so ladder length `s = sqrt{5.175^2+6.519^2} = 8.32 ft`

plot confirms authenticity of solution

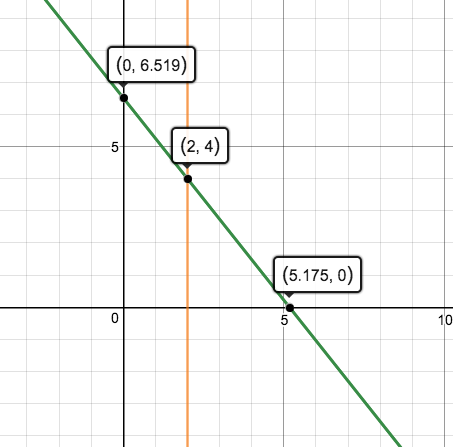
The "proof" that this is a minimum comes from physical arguments. It is easy to imagine a ladder that has its base a distance `epsilon` beyond the fence so that the similar triangles give

`y/(2 + epsilon) = 4 / epsilon |implies y = 8/epsilon + 4`

then `lim_{epsilon to oo} y = lim_{epsilon to oo} 8/epsilon + 4 = 4`

and `lim_{epsilon to 0} y = lim_{epsilon to 0} 8/epsilon + 4 = oo`

Answer 2

`8.32388` feet

Explanation:

Fence height = `h_0`
Fence distance = `d_0`
Ladder length = `l`

`l cos(alpha)= x + d_0`
`l sin(alpha) = y + h_0`
`(y+h_0)/h_0 = (x+d_0)/x` Thales of Miletus

Solving for `x,y,l` we have

#( (x = h_0 cot(alpha)), (y = d_0 tan(alpha)), (l = h_0/sin(alpha) + d_0/cos(alpha)) )#

Here `l(alpha)` so for stationary values determination we do

`(dl)/(d alpha) = -h_0 cos(alpha)/sin^2(alpha)+ d_0 sin(alpha)/cos^2(alpha) = 0`

or

`d_0sin^3(alpha)-h_0cos^3(alpha)=0 -> tan(alpha) = (h_0/d_0)^{1/3}`
`alpha = arctan[(h_0/d_0)^{1/3}] = 0.899908`

and

`l(0.899908)=8.32388` feet