Question

A feeding trough full of water is 5 ft long and its ends are isosceles triangles having a base and height of 3 ft. Water leaks out of the tank at a rate of 5 (ft)^3/min. How fast is the water level falling when the water in the tank is 6 in. deep?

Answer 1

falling at a rate of 2ft /min

Explanation:

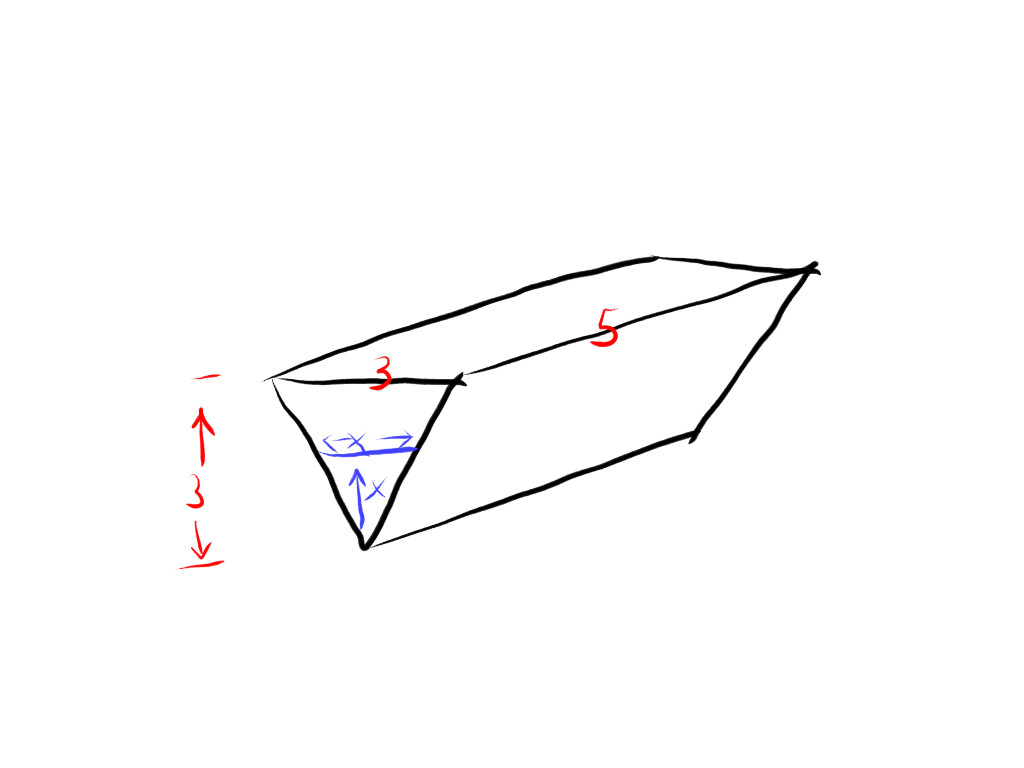
If you consider the generalised position when the depth of the water in the trough is at x where #x = x(t). Due to the similar triangles, the "width" of the water channel will also be x, as indicated in the drawing

We can say that the volume in the tank at that time, `V(t)`, is:

`V = 1/2 * x * x * l` where l is the length of the trough [ie 5 ft]

so `V = 5/2 x^2`

taking the derivative wrt time

`dot V = 5/2* 2 x * dot x = 5 x dot x` [where the dot is d/dt]

so `dot x = (dot V) / (5 x)`

we know that `dot V = - 5 (ft^3) /min` and we are asked about `dot x` at `x = 1/2 ft`

so so `dot x = (- 5 (ft^3) /min) / (5 ft * 1/2 ft) = - 2 (ft) /min`

so it's falling at a rate of 2ft /min at that moment